Next: 2 関数 Up: 1 数列と極限 Previous: 15 交項級数 Contents
16 絶対収束級数
定理 1.73 (絶対収束級数の収束定理)
級数 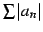 が収束するとき,級数
が収束するとき,級数 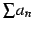 も収束する.
も収束する.
を考える. 絶対値の性質より
が成り立つ.これより
となる.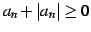 より
より
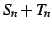 は正項級数である.
正項級数
は正項級数である.
正項級数 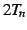 が収束するとき
が収束するとき
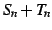 もまた収束する.
よって
もまた収束する.
よって 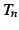 が収束するとき,
が収束するとき,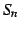 も収束する.
も収束する.
(証明)有限部分和
| (156) |
を考える. 絶対値の性質より
| (157) |
が成り立つ.これより
| (158) |
となる.
定義 1.74 (絶対収束級数)
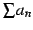 が収束し,かつ
が収束し,かつ
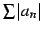 も収束するとき,
も収束するとき,
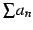 は絶対収束する(absolutely convergent)という.
このとき級数
は絶対収束する(absolutely convergent)という.
このとき級数
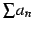 を
絶対収束級数(absolutely convergent series)と呼ぶ.
を
絶対収束級数(absolutely convergent series)と呼ぶ.
定義 1.75 (条件収束級数)
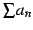 は収束するが
は収束するが
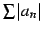 が収束しない場合は,
が収束しない場合は,
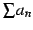 は条件収束する(conditionally convergent)という.
このとき級数
は条件収束する(conditionally convergent)という.
このとき級数
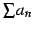 は
条件収束級数(conditionally convergent series)と呼ぶ.
は
条件収束級数(conditionally convergent series)と呼ぶ.
例 1.76 (絶対収束級数の具体例)
等比級数の例題で示したように
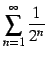 は収束する.
交項級数の例題で示したように
は収束する.
交項級数の例題で示したように
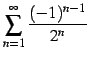 は収束する.
よって
は収束する.
よって
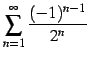 は
絶対収束級数である.
は
絶対収束級数である.
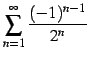 は収束する.
よって
は収束する.
よって
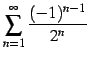 は
絶対収束級数である.
は
絶対収束級数である.
例 1.77 (条件収束級数の具体例)
交項級数
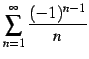 は
前述の例題で示したように収束する.
は
前述の例題で示したように収束する.
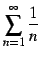 は調和級数であり
前述の例題のとおり発散する.
よって
は調和級数であり
前述の例題のとおり発散する.
よって
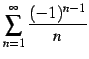 は
条件収束級数である.
は
条件収束級数である.
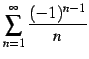 は
前述の例題で示したように収束する.
は
前述の例題で示したように収束する.
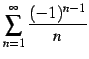 は
条件収束級数である.
は
条件収束級数である.
例 1.78 (絶対収束級数の収束定理の具体例)
級数
を考える. このとき
が成り立つ. ダランベールの判定法の例題で示したように,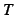 は収束する.
は収束する.
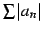 が収束するとき
が収束するとき
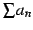 も収束するので,
も収束するので,
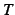 が収束するとき
が収束するとき 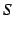 もまた収束する.
もまた収束する.
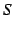 は絶対収束級数である.
は絶対収束級数である.
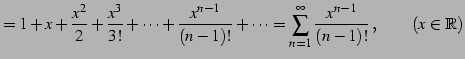 |
(159) |
を考える. このとき
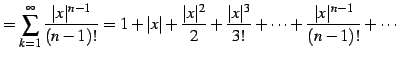 |
(160) |
が成り立つ. ダランベールの判定法の例題で示したように,
問 1.79
参考書(p.183)問題7-4.
Next: 2 関数 Up: 1 数列と極限 Previous: 15 交項級数 Contents
Kondo Koichi
Created at 2003/08/29