Next: 15 ちょっとまとめ Up: 3 微分法 Previous: 13 級の関数 Contents
14 接線の方程式
定義 3.43 (接線)
関数 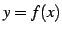 のグラフ上の点
のグラフ上の点 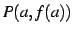 ,
,
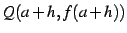 を
通る直線
を
通る直線 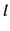 を考える.
極限
を考える.
極限 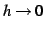 において直線
において直線 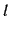 が直線
が直線 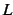 に近づくとする.
このとき直線
に近づくとする.
このとき直線 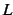 を
関数
を
関数 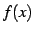 の点
の点 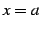 における接線(tangent)と呼ぶ.
における接線(tangent)と呼ぶ.
定理 3.44 (接線の方程式)
関数 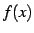 の点
の点 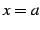 における接線の方程式は
における接線の方程式は
である.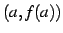 と
と
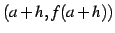 を通る直線の方程式は
を通る直線の方程式は
である.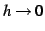 の極限をとると微分係数の定義より
の極限をとると微分係数の定義より
を得る.
| (498) |
である.
(証明) 点
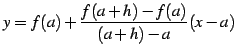 |
(499) |
である.
| (500) |
を得る.
注意 3.45 (関数の線形近似)
接線の方程式は点 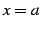 における関数
における関数 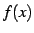 の
1 次(線形)近似ともいう.
ちなみに関数
の
1 次(線形)近似ともいう.
ちなみに関数 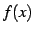 の
の 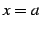 における
0 次近似は
における
0 次近似は 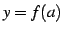 である.
である.
例 3.46 (接線の方程式の具体例)
関数 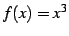 の点
の点 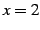 における接線の方程式は
における接線の方程式は
である.
| (501) |
である.
問 3.47
参考書(p.46)問題 3-2.
Kondo Koichi
Created at 2003/08/29