Next: 14 接線の方程式 Up: 3 微分法 Previous: 12 高階導関数 Contents
13 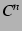 級の関数
級の関数
定理 3.39 (微分可能性と連続性)
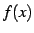 が
が 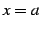 で微分可能なとき,
で微分可能なとき,
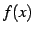 は
は 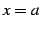 で連続である.
で連続である.
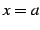 で微分が可能なので
で微分が可能なので
が成り立つ.これより
となる.ここで
とおく.このとき
である.(![[*]](./icons/crossref.png) )式を変形すると
)式を変形すると
となる.右辺を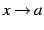 の極限をとる.
すると
の極限をとる.
すると
である.よって左辺も 0 となるので
を得る.よって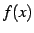 は
は 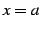 で連続である.
で連続である.
(証明) 点
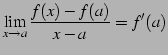 |
(490) |
が成り立つ.これより
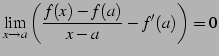 |
(491) |
となる.ここで
とおく.このとき
| (493) |
である.(
| (494) |
となる.右辺を
| (495) |
である.よって左辺も 0 となるので
| (496) |
を得る.よって
定義 3.40 (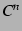 級関数)
級関数)
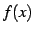 が連続関数のとき
が連続関数のとき 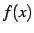 を
を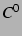 級の関数という.
関数
級の関数という.
関数 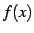 が
が 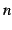 回微分可能であり,
回微分可能であり,
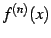 が連続関数であるとき,
が連続関数であるとき,
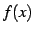 を
を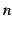 回連続微分可能な関数といい,
回連続微分可能な関数といい,
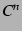 級の関数という.
また何回でも微分が可能な関数を
無限回微分可能な関数といい,
級の関数という.
また何回でも微分が可能な関数を
無限回微分可能な関数といい,
 級の関数という.
級の関数という.
例 3.41 (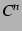 級関数の具体例)
多項式関数,
級関数の具体例)
多項式関数,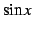 ,
, 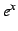 は
は  級の関数である.
級の関数である.
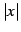 は
は 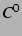 級の関数である.
級の関数である.
注意 3.42 (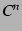 級関数の集合)
級関数の集合)
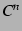 級の関数全体の集合を
級の関数全体の集合を 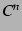 と書くとする.
このとき
と書くとする.
このとき
が成り立つ.
| (497) |
が成り立つ.
Next: 14 接線の方程式 Up: 3 微分法 Previous: 12 高階導関数 Contents
Kondo Koichi
Created at 2003/08/29