Next: 4 テイラー級数 Up: 3 微分法 Previous: 14 接線の方程式 Contents
15 ちょっとまとめ
|
|
|
|
|
|
|
|
0 | 0 | 0 | 0 |
|
|
|
|
|
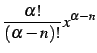 (
(
|
|
(
|
0 (
|
|||
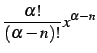 (
(
|
||||
|
|
|
|||
|
|
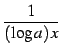 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
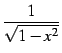 |
|||
|
|
 |
|||
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|||
|
|
 |
|||
|
|
 |
|||
|
|
|
問 3.48
上の表の空いている個所を埋めよ.
Next: 4 テイラー級数 Up: 3 微分法 Previous: 14 接線の方程式 Contents
Kondo Koichi
Created at 2003/08/29