Next: 16 絶対収束級数 Up: 1 数列と極限 Previous: 14 正項級数の収束性判定法 Contents
15 交項級数
定義 1.69 (交項級数)
級数
を交項級数(alternative term series)と呼ぶ.
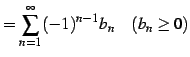 |
(151) |
を交項級数(alternative term series)と呼ぶ.
定理 1.70 (交項級数の収束定理)
交項級数
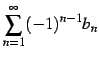 は
次の条件を満たすとき収束する:
は
次の条件を満たすとき収束する:
はと書ける.条件より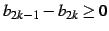 となるので,
となるので,
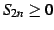 となる.
また
となる.
また
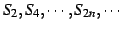 は単調増加となる.
さらには
は単調増加となる.
さらには 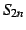 は
は
とも書ける.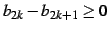 ,
,
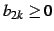 であるから,
であるから,
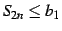 となる.よって
となる.よって 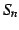 は
は
を満たす.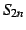 は有界な単調増加数列である.
よって
は有界な単調増加数列である.
よって 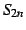 は極限
は極限
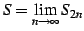 が存在する.
次に
が存在する.
次に 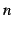 が奇数にる場合を考える.
が奇数にる場合を考える.
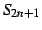 の極限は
の極限は
と得られる.以上で証明終了.
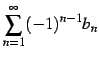 は
次の条件を満たすとき収束する:
は
次の条件を満たすとき収束する:
- (i)
-
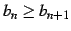 .
.
- (ii)
-
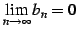 .
.
(証明)![]() が偶数のときの有限部分和
が偶数のときの有限部分和
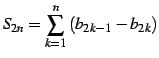 |
(152) |
はと書ける.条件より
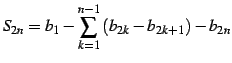 |
(153) |
とも書ける.
| (154) |
を満たす.
| (155) |
と得られる.以上で証明終了.
例 1.71 (交項級数の収束定理の具体例)
級数
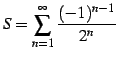 は
収束する.
なぜなら
は
収束する.
なぜなら
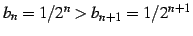 であり,
であり,
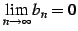 であるから,
定理より級数は収束する.
であるから,
定理より級数は収束する.
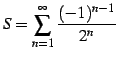 は
収束する.
なぜなら
は
収束する.
なぜなら
例 1.72 (交項級数の収束定理の具体例)
級数
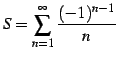 は
収束する.
なぜなら
は
収束する.
なぜなら
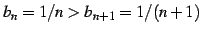 であり,
であり,
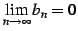 であるから,
定理より級数は収束する.
であるから,
定理より級数は収束する.
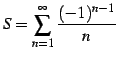 は
収束する.
なぜなら
は
収束する.
なぜなら
Kondo Koichi
Created at 2003/08/29