3.12 演習問題 〜 多重積分の積分変数の変換
問 3.59 (積分変数の変換)
次の多重積分を置換積分により求めよ.
(1)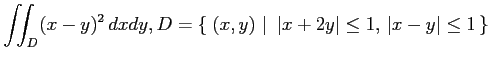
(2)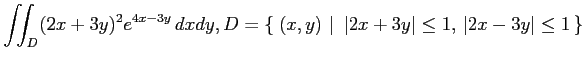
(3)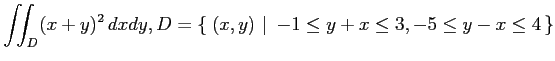
(4)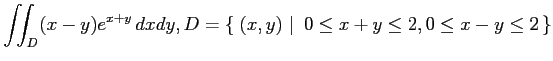
(1)
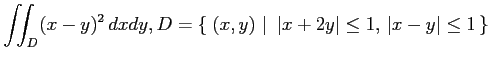
(2)
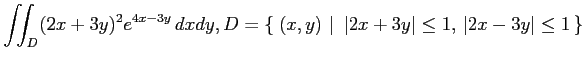
(3)
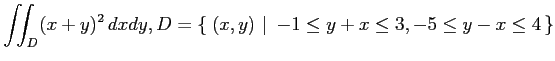
(4)
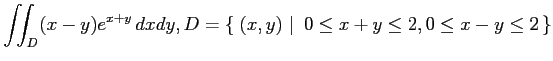
問 3.60 (積分変数の変換)
次の多重積分を置換積分により求めよ.
(1)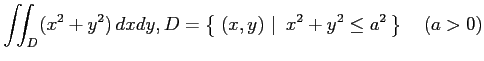
(2)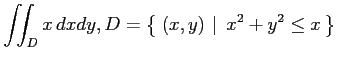
(3)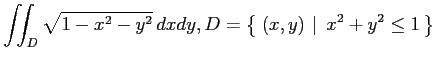
(4)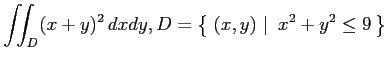
(5)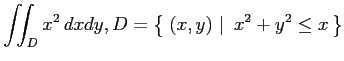
(6)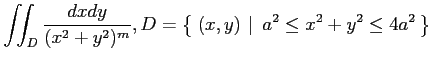
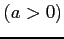
(1)
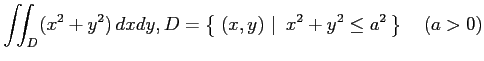
(2)
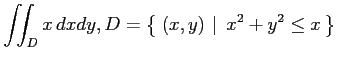
(3)
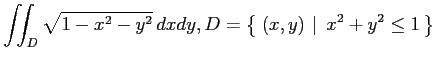
(4)
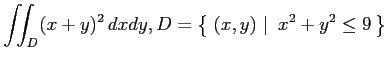
(5)
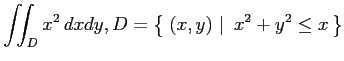
(6)
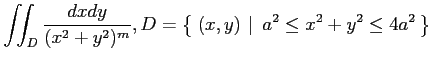
問 3.61 (積分変数の変換)
次の多重積分を置換積分により求めよ.
(1)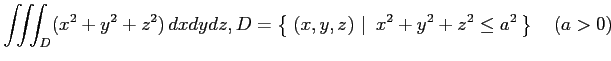
(2)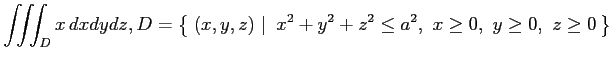
(3)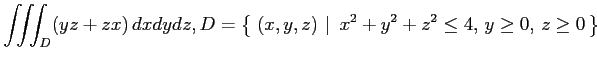
(1)
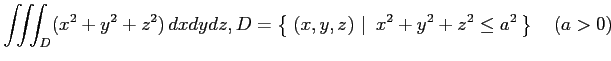
(2)
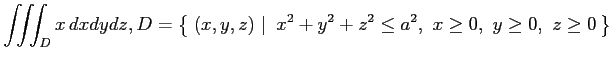
(3)
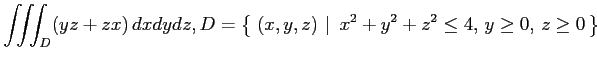
問 3.62 (積分変数の変換)
次の多重積分を置換積分により求めよ.
(1)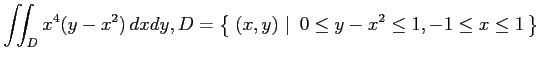
(ヒント: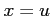 ,
,
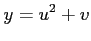 )
)
(2)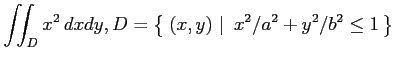 (
(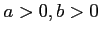 )
)
(ヒント: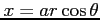 ,
,
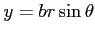 )
)
(3)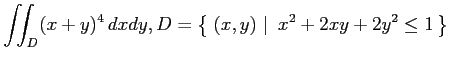
(ヒント: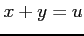 ,
,
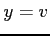 )
)
(1)
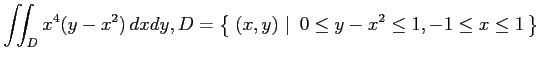
(ヒント:
(2)
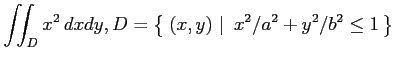 (
((ヒント:
(3)
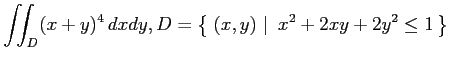
(ヒント:
平成21年12月2日