2.28 演習問題 〜 単位ベクトル,正射影,点と直線の距離
問 2.86 (正射影)
点 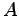 から直線
から直線 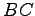 への正射影
への正射影 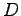 を求めよ.
また距離
を求めよ.
また距離 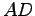 を求めよ.
を求めよ.
(1)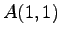 ,
, 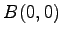 ,
, 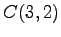 (2)
(2) 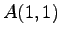 ,
, 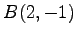 ,
, 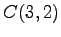
(3)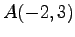 ,
, 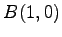 ,
, 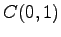 (4)
(4) 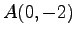 ,
, 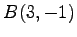 ,
, 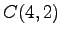
(5)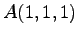 ,
, 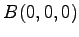 ,
, 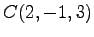 (6)
(6) 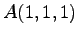 ,
, 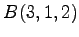 ,
, 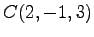
(7)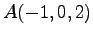 ,
, 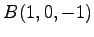 ,
, 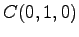 (8)
(8) 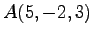 ,
, 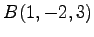 ,
, 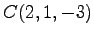
(1)
(3)
(5)
(7)
問 2.87 (正射影)
点 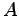 と直線
と直線 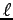 の距離を求めよ.
の距離を求めよ.
(1)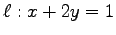 ,
, 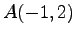 (2)
(2)
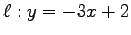 ,
, 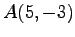
(3)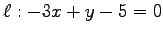 ,
, 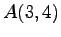 (4)
(4)
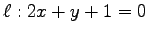 ,
, 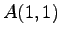
(5)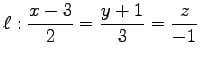 ,
, 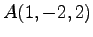 (6)
(6)
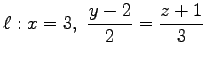 ,
, 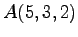
(7)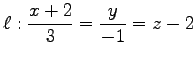 ,
, 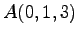 (8)
(8)
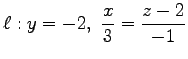 ,
, 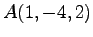
(1)
(3)
(5)
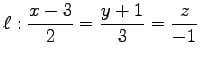 ,
, 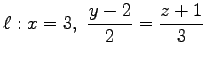 ,
, (7)
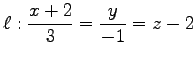 ,
, 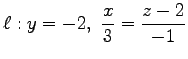 ,
,
問 2.88 (点と直線の距離)
点 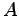 と直線
と直線 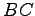 の距離を求めよ.
の距離を求めよ.
(1)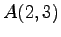 ,
, 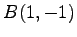 ,
, 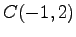 (2)
(2) 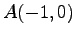 ,
, 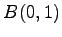 ,
, 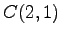
(3)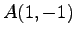 ,
, 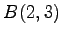 ,
, 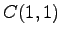 (4)
(4) 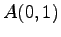 ,
, 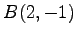 ,
, 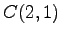
(5)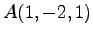 ,
, 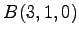 ,
, 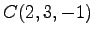 (6)
(6) 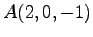 ,
, 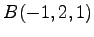 ,
, 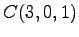
(7)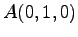 ,
, 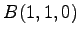 ,
, 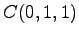 (8)
(8) 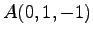 ,
, 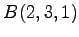 ,
, 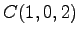
(1)
(3)
(5)
(7)
平成20年4月22日