2.23 点の平面への正射影
定義 2.53 (点の平面への正射影)
点 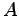 から平面へ垂線を下ろしたときの足
から平面へ垂線を下ろしたときの足 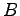 を正射影という.
点
を正射影という.
点 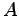 から点
から点 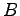 への変換を射影変換という.
への変換を射影変換という.
例 2.54 (点の平面への正射影)
点 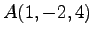 の平面
の平面
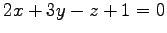 への正射影
への正射影 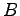 を考える.
平面の法線ベクトルは
を考える.
平面の法線ベクトルは
![$ \vec{n}=\begin{bmatrix}{2}\\ [-.5ex]{3}\\ [-.5ex]{-1}\end{bmatrix}$](img398.png) であるから,
点
であるから,
点 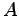 を通り平面に垂直な直線の方程式は
を通り平面に垂直な直線の方程式は
となる. パラメータ表示すると
である. これを平面の方程式に代入すると
より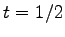 を得る.
これを垂線の方程式に代入すると
を得る.
これを垂線の方程式に代入すると
であり,正射影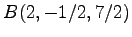 を得る.
を得る.
![$ \vec{n}=\begin{bmatrix}{2}\\ [-.5ex]{3}\\ [-.5ex]{-1}\end{bmatrix}$](img398.png) であるから,
点
であるから,
点 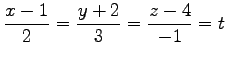 |
(95) |
となる. パラメータ表示すると
| (96) |
である. これを平面の方程式に代入すると
| (97) |
より
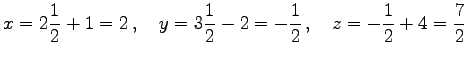 |
(98) |
であり,正射影
平成20年4月22日