2.18 点と直線との距離
定義 2.41 (点と直線との距離)
点 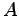 と
と 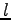 上の点
上の点 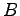 との距離が最小となるとき,
その距離を点と直線との距離という.
との距離が最小となるとき,
その距離を点と直線との距離という.
定理 2.42 (点と直線との距離)
点 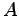 と
と 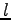 上の点
上の点 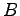 との距離が最小となるのは,
直線
との距離が最小となるのは,
直線 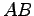 と直線
と直線 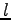 が直交するときである.
が直交するときである.
定理 2.43 (
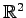 内の点と直線の距離)
内の点と直線の距離)
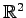 空間内の点
空間内の点
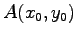 と
直線
と
直線 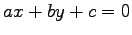 との距離は
との距離は
である.
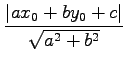 |
(81) |
である.
問 2.44 (
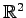 内の点と直線の距離)
これを示せ.
内の点と直線の距離)
これを示せ.
問 2.45 (
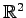 内の点と直線の距離)
点
内の点と直線の距離)
点 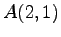 と直線
と直線 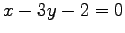 との距離は
との距離は
である.
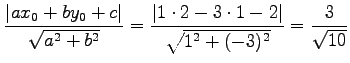 |
(82) |
である.
平成20年4月22日