3.16 演習問題 〜 体積,曲面積
問 3.75 (体積)
次の立体の体積を多重積分を用いて求めよ.
(1) 半径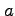 の球.
(2) 底面の半径
の球.
(2) 底面の半径 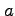 ,高さ
,高さ 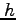 の円柱.
(3) 底面の半径
の円柱.
(3) 底面の半径 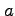 ,高さ
,高さ 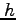 の円錐.
の円錐.
(4) 半球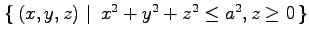 と
円柱
と
円柱
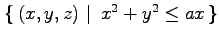 の共通部分.
の共通部分.
(5) 球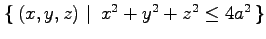 から
円柱
から
円柱
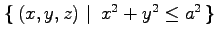 を除いた領域.
を除いた領域.
(6) 円柱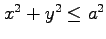 の
の
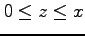 の領域.
の領域.
(7) 2 つの円柱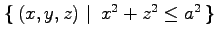 ,
,
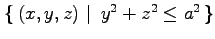 の共通部分.
の共通部分.
(8) 曲面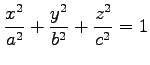
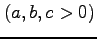 に囲まれた領域.
に囲まれた領域.
(9) 曲面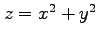 と平面
と平面 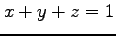 に囲まれた領域.
に囲まれた領域.
(10) 円柱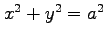
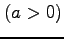 と 2 平面
と 2 平面 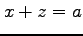 ,
, 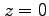 に囲まれた領域.
に囲まれた領域.
(11) 曲面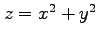 , 円柱
, 円柱 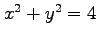 および
平面
および
平面 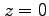 に囲まれた領域.
に囲まれた領域.
(12) 曲面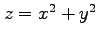 と平面
と平面 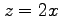 に囲まれた領域.
に囲まれた領域.
(13) 曲面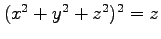 で囲まれた領域.
で囲まれた領域.
(14) 曲面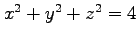 ,
,
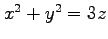 に囲まれた領域.
に囲まれた領域.
(1) 半径
(4) 半球
(5) 球
(6) 円柱
(7) 2 つの円柱
(8) 曲面
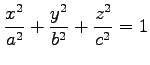
(9) 曲面
(10) 円柱
(11) 曲面
(12) 曲面
(13) 曲面
(14) 曲面
問 3.76 (曲面積)
次の曲面の曲面積を求めよ.ただし 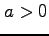 とする.
とする.
(1) 半径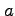 の球の表面.
(2) 球面
の球の表面.
(2) 球面
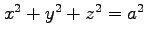 の
の
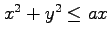 ,
, 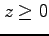 の部分.
の部分.
(3)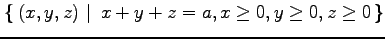 (4)
(4)
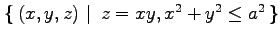
(5)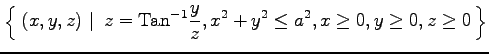
(6)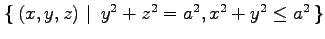 (7)
(7)
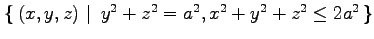
(8)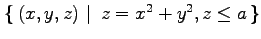 (9) 曲面
(9) 曲面 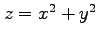 と平面
と平面 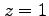 で囲まれる図形.
で囲まれる図形.
(10) 球面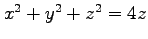 のうち曲面
のうち曲面 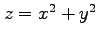 の内部にある部分.
の内部にある部分.
(11) 曲面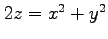 のうち円柱
のうち円柱 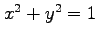 の内部にある部分.
の内部にある部分.
(12) 球面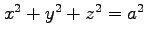 の
の 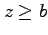 の部分
の部分 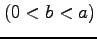 .
.
(1) 半径
(3)
(5)
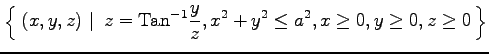
(6)
(8)
(10) 球面
(11) 曲面
(12) 球面
問 3.77 (体積)
下図の三角錐について,次の問に答えよ.
(1)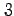 点
点 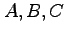 を通る平面
を通る平面 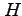 の方程式を(i)-(iii)の方法で求めよ.
の方程式を(i)-(iii)の方法で求めよ.
(i) 平面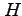 を一般形
を一般形
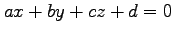 で表し
で表し 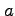 ,
, 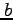 ,
, 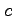 ,
, 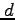 に関して解いて求めよ.
に関して解いて求めよ.
(ii) 平面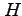 を
を
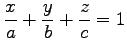 と
おいて
と
おいて 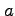 ,
, 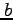 ,
, 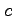 に関して解いて求めよ.
に関して解いて求めよ.
(iii) 平面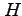 の法線ベクトルを
の法線ベクトルを
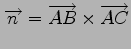 により求めて
により求めて 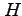 の方程式を求めよ.
の方程式を求めよ.
(2) 底面の領域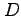 を
を 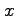 に関して単純な式で表せ.
に関して単純な式で表せ.
(3) 底面の領域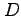 の面積
の面積
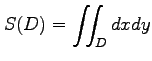 を計算せよ.
を計算せよ.
(4) 平面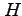 の方程式を
の方程式を 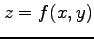 の形で表せ.
の形で表せ.
(5) 三角錐の体積を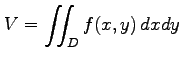 で計算せよ.
で計算せよ.
(6) 三角形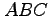 の面積を
の面積を
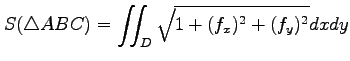 により求めよ.
により求めよ.
![\includegraphics[width=0.4\textwidth]{enshu/tri.eps}](img2422.png)
(1)
(i) 平面
(ii) 平面
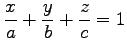 と
おいて
と
おいて (iii) 平面
(2) 底面の領域
(3) 底面の領域
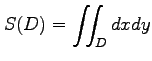 を計算せよ.
を計算せよ.
(4) 平面
(5) 三角錐の体積を
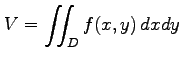 で計算せよ.
で計算せよ.
(6) 三角形
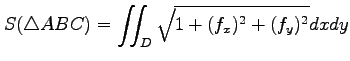 により求めよ.
により求めよ.
![\includegraphics[width=0.4\textwidth]{enshu/tri.eps}](img2422.png)
問 3.78 (多重積分の広義積分への応用)
次を示せ.
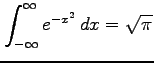 |
平成21年1月14日