3.14 曲面積
定理 3.71 (曲面積)
関数 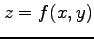 による曲面
による曲面
の曲面積は
で与えられる.
の曲面積は
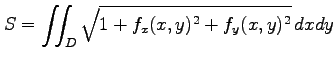 |
で与えられる.
例 3.72 (球面の表面積)
半径 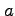 の球面は
の球面は
である.表面積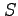 は 8 等分して
は 8 等分して
により求まる.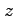 は
は
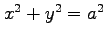 により定まる陰関数であるから,
により定まる陰関数であるから,
となる. 被積分関数は
であらから,表面積は
と得られる.
である.表面積
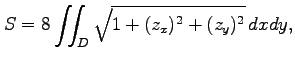 |
||
により求まる.
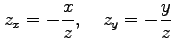 |
となる. 被積分関数は
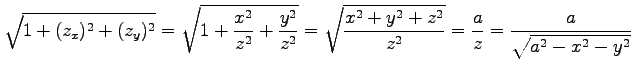 |
であらから,表面積は
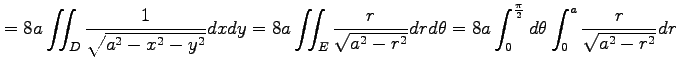 |
||
![$\displaystyle = 8a \left[\vrule height1.5em width0em depth0.1em\,{\theta}\,\rig...
...rule height1.5em width0em depth0.1em\,{-\sqrt{a^2-r^2}}\,\right]_0^a = 4\pi a^2$](img2352.png) |
と得られる.
例 3.73 (曲面積)
曲面
の曲面積
を求める.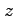 は
は
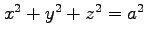 により定まる陰関数であるから,
により定まる陰関数であるから,
となり,
を得る.これを用いると曲面積は
と求まる.
の曲面積
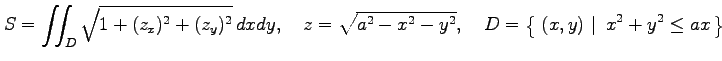 |
を求める.
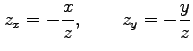 |
となり,
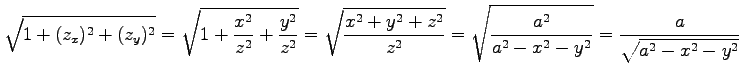 |
を得る.これを用いると曲面積は
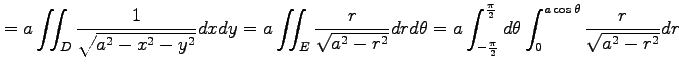 |
||
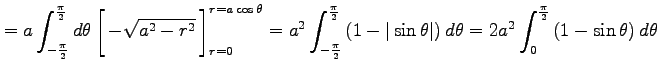 |
||
![$\displaystyle = 2a^2 \left[\vrule height1.5em width0em depth0.1em\,{\theta+\cos\theta}\,\right]_{0}^{\frac{\pi}{2}} = (\pi-2)a^2$](img2360.png) |
と求まる.
平成21年1月14日