2.37 演習問題 〜 テイラー展開
問 2.159 (テイラー展開)
関数 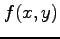 を点
を点 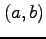 のまわりで点
のまわりで点 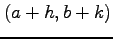 について
について
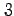 次項までテイラー展開せよ.
ただし,剰余項も具体的に書き下して表せ.
次項までテイラー展開せよ.
ただし,剰余項も具体的に書き下して表せ.
問 2.160 (テイラー展開)
次の関数 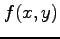 を点
を点 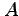 のまわりで
点
のまわりで
点 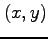 についてテイラー展開せよ.
についてテイラー展開せよ.
(1)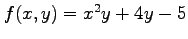 ,
, 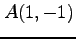
(2)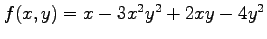 ,
, 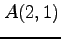
(3)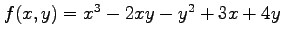 ,
, 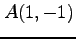
(4)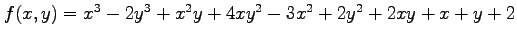 ,
, 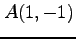
(1)
(2)
(3)
(4)
問 2.161 (テイラー展開)
次の関数 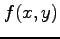 を原点
を原点 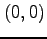 のまわりで
点
のまわりで
点 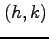 について
について 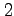 次項までテイラー展開せよ.
ただし,剰余項も具体的に書き下して表せ.
次項までテイラー展開せよ.
ただし,剰余項も具体的に書き下して表せ.
(1)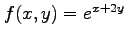 (2)
(2)
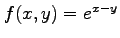 (3)
(3)
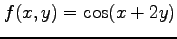
(1)
問 2.162 (テイラー展開)
次の関数 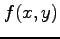 を点
を点 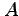 のまわりで点
のまわりで点 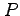 について
について
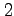 次項までテイラー展開せよ.
次項までテイラー展開せよ.
(1)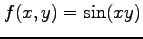 ,
,
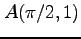 ,
, 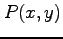
(2)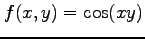 ,
, 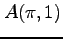 ,
,
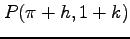
(3)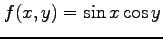 ,
,
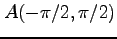 ,
,
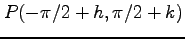
(1)
(2)
(3)
問 2.163 (テイラー展開)
次の関数 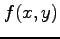 を 1 次項までマクローリン展開せよ.
ただし,剰余項も具体的に書き下して表せ.
を 1 次項までマクローリン展開せよ.
ただし,剰余項も具体的に書き下して表せ.
(1)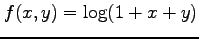 (2)
(2)
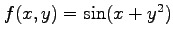 (3)
(3)
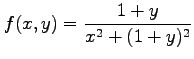
(1)
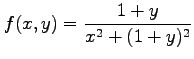
平成21年1月14日