2.27 座標変換
定義 2.114 (座標変換)
座標
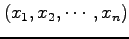 が
変数
が
変数
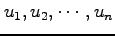 を独立変数とする関数
を独立変数とする関数
により定まるとする. このとき,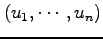 をあらたに座標と呼び,
(*)を座標
をあらたに座標と呼び,
(*)を座標
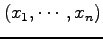 から
座標
から
座標
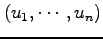 への
座標変換(coordinate transform)と呼ぶ.
への
座標変換(coordinate transform)と呼ぶ.
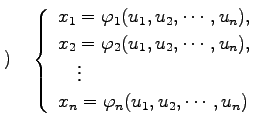 |
により定まるとする. このとき,
平成21年1月14日
2.27 座標変換
定義 2.114 (座標変換) 座標が 変数
を独立変数とする関数
*
により定まるとする. このとき,をあらたに座標と呼び, (*)を座標
から 座標
への 座標変換(coordinate transform)と呼ぶ.
平成21年1月14日