2.25 偏微分作用素
例 2.105 (偏微分作用素)
関数 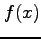 の 1 階偏導関数は
の 1 階偏導関数は
と表される.微分するという操作
を偏微分作用素(演算子) (partial differential operator)という.
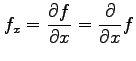 |
と表される.微分するという操作
を偏微分作用素(演算子) (partial differential operator)という.
例 2.106 (高階微分)
関数 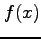 の 2 階偏導関数は
の 2 階偏導関数は
と表される.関数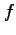 は任意であるから
偏微分作用素のみを抜き出すと
は任意であるから
偏微分作用素のみを抜き出すと
と表される. 同様にして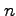 階偏導関数は
階偏導関数は
と表される.関数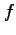 は任意であるから
は任意であるから
が成り立つ.
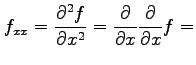 |
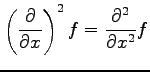 |
と表される.関数
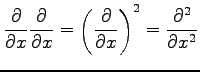 |
と表される. 同様にして
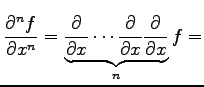 |
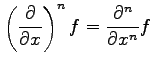 |
と表される.関数
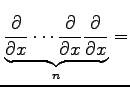 |
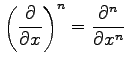 |
が成り立つ.
例 2.107 (線形結合の微分)
関数 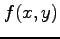 の
の 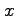 と
と 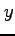 に関する 1 階偏導関数の線形結合は
に関する 1 階偏導関数の線形結合は
と表される. 関数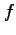 は任意であるから
は任意であるから
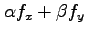 の作用素は
の作用素は
である.
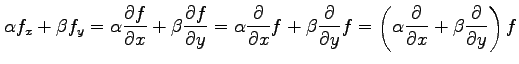 |
と表される. 関数
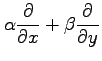 |
である.
例 2.108 (2 項展開)
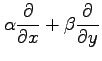 を 2 回繰り返す作用素は
を 2 回繰り返す作用素は
と表される.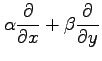 を
を 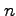 回繰り返す作用素は
回繰り返す作用素は
と表される.
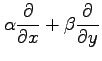 を 2 回繰り返す作用素は
を 2 回繰り返す作用素は
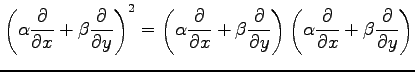 |
||
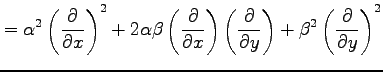 |
||
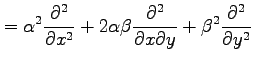 |
と表される.
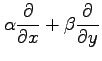 を
を 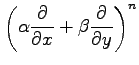 |
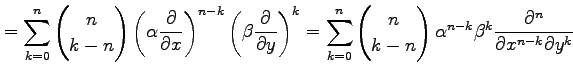 |
と表される.
例 2.109 (積の微分)
関数 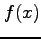 ,
, 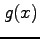 に対して
に対して
が成り立つ.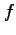 は任意であるから,
は任意であるから,
と書ける.
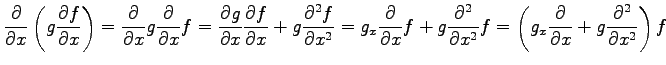 |
が成り立つ.
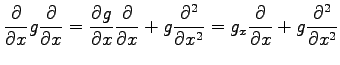 |
と書ける.
例 2.110 (関数係数の 2 項展開)
偏微分作用素
を 2 回繰り返すと
となる.
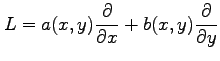 |
を 2 回繰り返すと
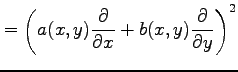 |
||
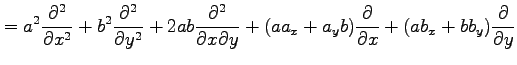 |
となる.
平成21年1月14日