1.4 区間
定義 1.11 (区間)
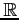 の部分集合
の部分集合 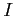 を区間(interval)といい,
を区間(interval)といい,
と表記する.特に,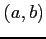 を開区間(open interval),
を開区間(open interval),
![$ [a,b]$](img62.png) を閉区間(closed interval)という.
を閉区間(closed interval)という.
と表記する.特に,
例 1.12 (開区間の例)
平成21年6月1日
1.4 区間
定義 1.11 (区間)の部分集合
を区間(interval)といい,
と表記する.特に,を開区間(open interval),
を閉区間(closed interval)という.
例 1.12 (開区間の例)
平成21年6月1日