6.11 有理関数の積分 〜 部分分数の積分
例 6.56 (部分分数の積分の計算例)
Type 1:
Type 2:
Type 3:
Type 4:
Type 5:
Type 6: これはあとの例題で示す.
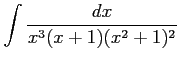 |
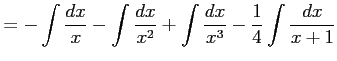 |
|
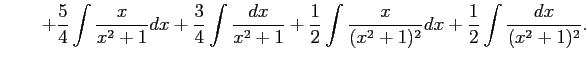 |
Type 1:
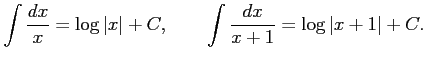 |
Type 2:
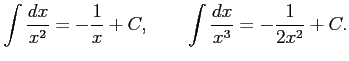 |
Type 3:
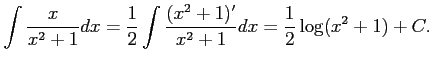 |
Type 4:
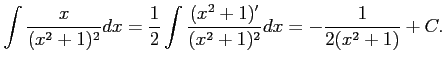 |
Type 5:
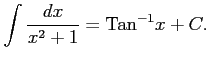 |
Type 6: これはあとの例題で示す.
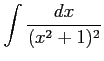 |
例 6.57 (有理式関数の不定積分の具体例)
(Type 1 のみ)
不定積分
を計算する. まず,部分分数分解する.
とおき,通分し分子を比較すると
となる. これに,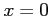 を代入すると
を代入すると
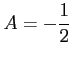 を得る.
を得る.
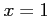 を代入すると
を代入すると
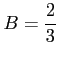 を得る.
を得る.
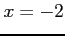 を代入すると
を代入すると
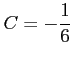 を得る.
よって
を得る.
よって
となる. これを積分して
を得る.
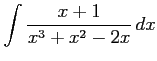 |
を計算する. まず,部分分数分解する.
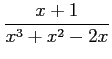 |
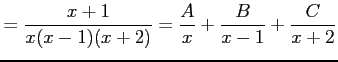 |
とおき,通分し分子を比較すると
となる. これに,
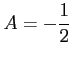 を得る.
を得る.
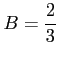 を得る.
を得る.
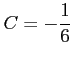 を得る.
よって
を得る.
よって
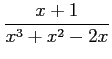 |
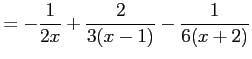 |
となる. これを積分して
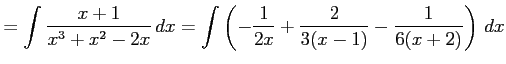 |
||
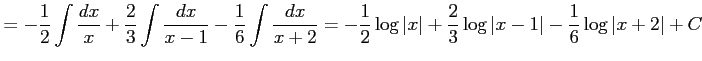 |
||
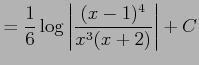 |
を得る.
例 6.58 (有理式関数の不定積分の具体例)
(Type 1, 3, 5)
不定積分
を計算する.まず, 部分分数分解として
とする. 通分して分子を比較すると
となる. これに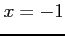 ,
, 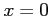 ,
, 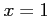 をそれぞれ代入すると,
をそれぞれ代入すると,
となる. これを解くと
を得る. よって部分分数分解は
と表される. よって,
を得る.
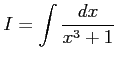 |
を計算する.まず, 部分分数分解として
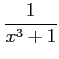 |
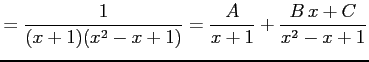 |
とする. 通分して分子を比較すると
となる. これに
となる. これを解くと
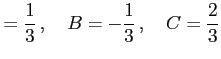 |
を得る. よって部分分数分解は
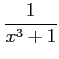 |
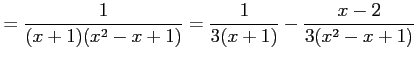 |
と表される. よって,
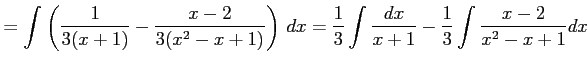 |
||
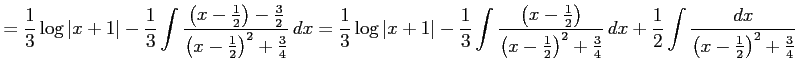 |
||
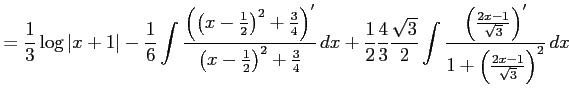 |
||
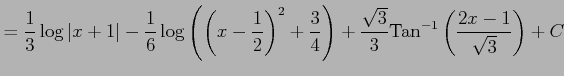 |
||
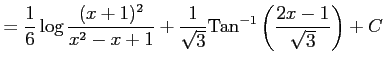 |
を得る.
例 6.59 (有理式関数の不定積分の具体例)
(Type 1, 3, 5)
不定積分
を計算する. まず
とおき,通分し分子を比較すると,恒等式
を得る. これに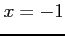 ,
, 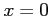 ,
, 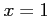 をそれぞれ代入すると
をそれぞれ代入すると
となる. これを解くと
を得る.よって
となる.これより
を得る.
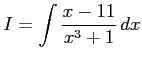 |
を計算する. まず
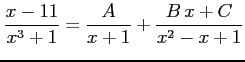 |
とおき,通分し分子を比較すると,恒等式
を得る. これに
となる. これを解くと
を得る.よって
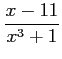 |
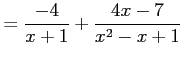 |
となる.これより
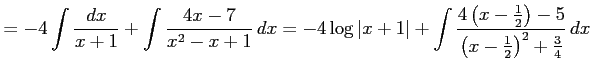 |
||
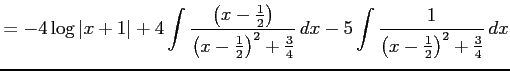 |
||
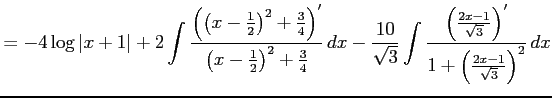 |
||
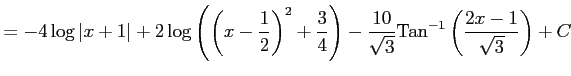 |
||
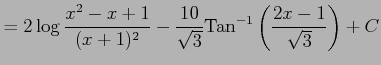 |
を得る.
例 6.60 (有理式関数の不定積分の具体例)
(Step1, Type 3, 5)
不定積分
を計算する. 分子の次数が分母の次数以上であるから, 分子を分母で割り
のように変形する. 多項式部分は積分される. 残るは有理式の積分である. これを計算すると
となる. よって
を得る.
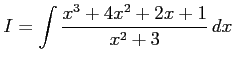 |
を計算する. 分子の次数が分母の次数以上であるから, 分子を分母で割り
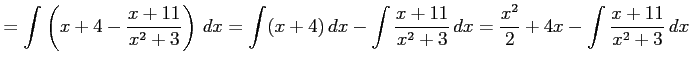 |
のように変形する. 多項式部分は積分される. 残るは有理式の積分である. これを計算すると
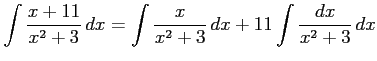 |
||
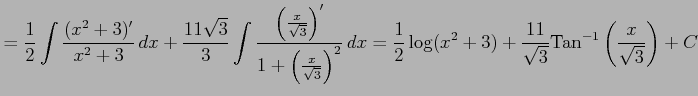 |
となる. よって
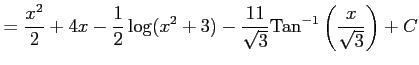 |
を得る.
例 6.61 (有理式関数の不定積分の具体例)
(Type 6)
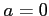 ,
,  の場合の
の場合の 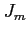 を求める.
を求める.
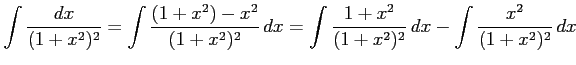 |
||
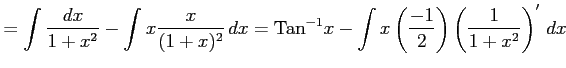 |
||
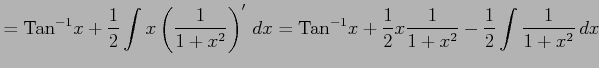 |
||
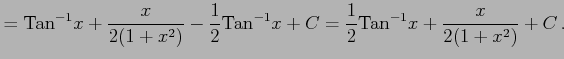 |
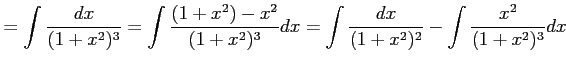 |
||
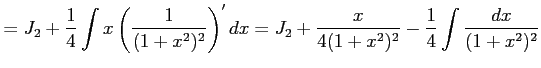 |
||
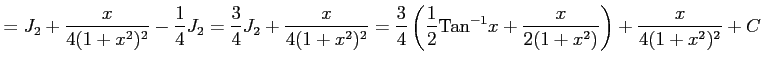 |
||
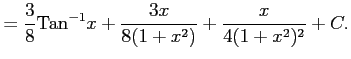 |
例 6.62 (有理式の積分)
(Type 5)
不定積分
を計算する. 被積分関数の有理式の分母が 0 となるのは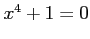 のときだから,
代数方程式
のときだから,
代数方程式 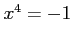 を複素解も含めて解くと,
を複素解も含めて解くと,
となる. 複素解を順に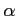 ,
,
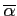 ,
,
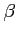 ,
,
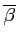 とおくと,
分母は
とおくと,
分母は
と因数分解される. 被積分関数の有理式を部分分数分解すると,
とおける.右辺を通分するとその分子は,
となるので,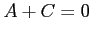 ,
,
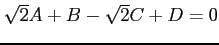 ,
,
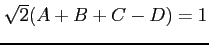 ,
,
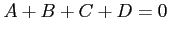 とおいて解くと,
とおいて解くと,
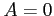 ,
,
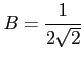 ,
,
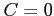 ,
,
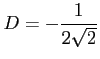 を得る.よって
を得る.よって
と書ける. よって積分は
となる. ここで,
をみたす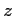 を
を 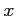 ,
, 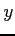 で表す.
で表す.
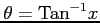 ,
,
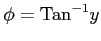 ,
,
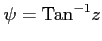 とおくと,
とおくと,
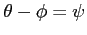 となるので,
両辺に
となるので,
両辺に 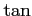 を作用させると,
を作用させると,
を得る.これを用いると,
となる. また,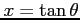 とすると,
とすると,
となるので,
を得る.
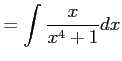 |
を計算する. 被積分関数の有理式の分母が 0 となるのは
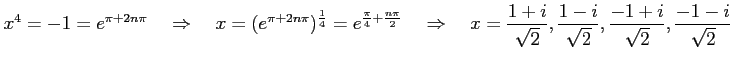 |
となる. 複素解を順に
と因数分解される. 被積分関数の有理式を部分分数分解すると,
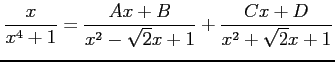 |
とおける.右辺を通分するとその分子は,
となるので,
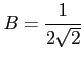 ,
,
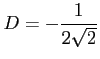 を得る.よって
を得る.よって
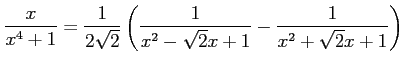 |
と書ける. よって積分は
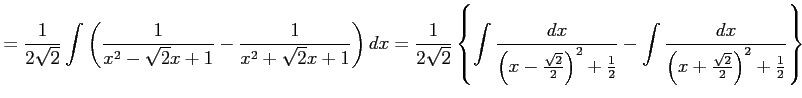 |
||
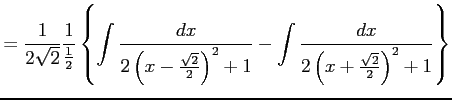 |
||
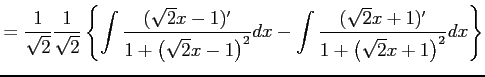 |
||
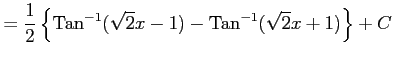 |
となる. ここで,
をみたす
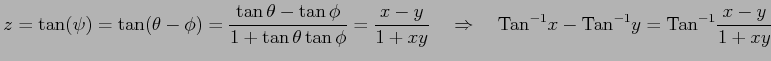 |
を得る.これを用いると,
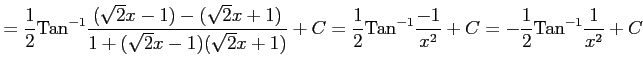 |
となる. また,
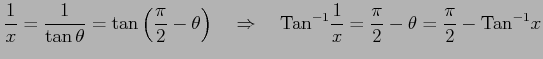 |
となるので,
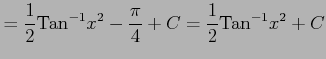 |
を得る.
平成21年6月1日