6.10 有理関数の積分 〜 部分分数分解
例 6.53 (部分分数展開の具体例)
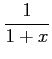 |
||
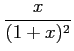 |
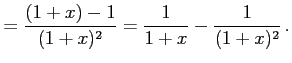 |
|
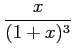 |
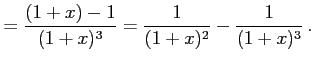 |
|
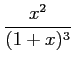 |
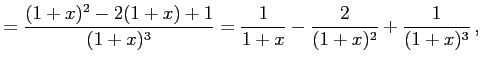 |
|
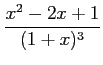 |
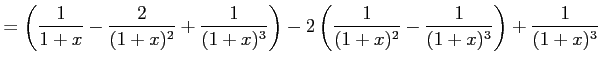 |
|
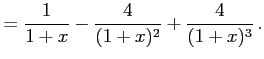 |
例 6.54 (部分分数展開の計算例)
部分分数分解
を行う. 係数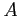 ,
, 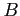 ,
, 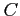 ,
, 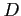 を決定する.
通分し分子を比較すると
を決定する.
通分し分子を比較すると
となる. これは恒等式であるから, どの実数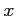 に対しても成立する必要がある.
例えば,
に対しても成立する必要がある.
例えば,
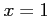 ,
, 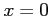 ,
, 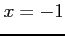 ,
, 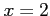 をそれぞれ代入すると
をそれぞれ代入すると
を得る. これを解くと
となる. よって,
を得る.
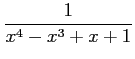 |
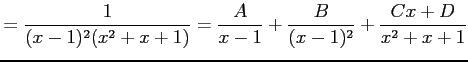 |
を行う. 係数
となる. これは恒等式であるから, どの実数
を得る. これを解くと
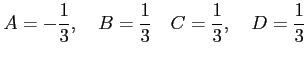 |
となる. よって,
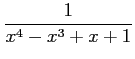 |
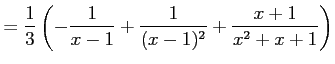 |
を得る.
例 6.55 (部分分数展開の計算例)
部分分数分解
を行う. 係数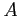 ,
, 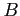 ,
, 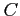 ,
, 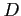 ,
, 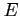 ,
, 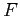 ,
, 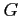 ,
, 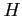 を決定する.
通分し分子の比較をすると,
を決定する.
通分し分子の比較をすると,
となる. これは恒等式であるから, すべての実数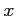 および複素数
および複素数 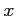 に対しても成立する必要がある.
例えば,
に対しても成立する必要がある.
例えば,
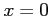 ,
, 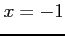 ,
, 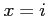 をそれぞれ代入すると
をそれぞれ代入すると
となる. これを解くと,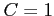 ,
,
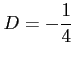 ,
,
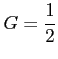 ,
,
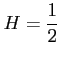 を得る.
恒等式を展開し同じ次数でまとめると
を得る.
恒等式を展開し同じ次数でまとめると
となる.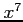 ,
, 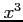 ,
, 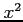 ,
, 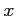 の係数を比較すると
の係数を比較すると
となる. これを解くと
を得る.よって,
となる.
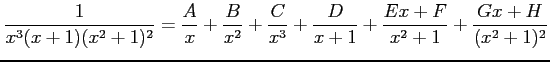 |
を行う. 係数
となる. これは恒等式であるから, すべての実数
となる. これを解くと,
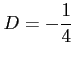 ,
,
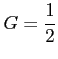 ,
,
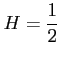 を得る.
恒等式を展開し同じ次数でまとめると
を得る.
恒等式を展開し同じ次数でまとめると
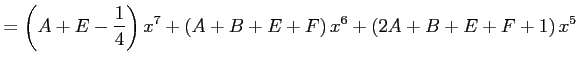 |
||
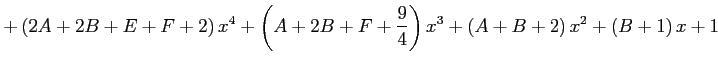 |
となる.
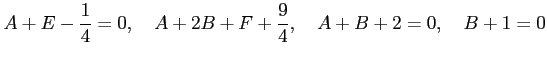 |
となる. これを解くと
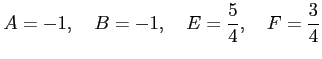 |
を得る.よって,
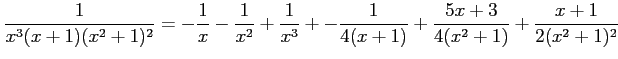 |
となる.
平成21年6月1日