2.2 写像の分類
定義 2.7 (全射)
写像 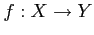 において,
において,
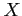 のすべての元が
のすべての元が 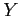 のすべての元に対応づけられているとき,
のすべての元に対応づけられているとき,
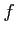 を上への写像(onto mapping)または
全射(subjection)という.
ただし
を上への写像(onto mapping)または
全射(subjection)という.
ただし 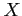 の複数の元が
の複数の元が 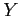 の同じ元へ対応づけられていてもよい.
の同じ元へ対応づけられていてもよい.
定義 2.8 (単射)
写像 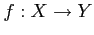 において,
において,
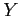 の元への対応が重ならないとき,
の元への対応が重ならないとき,
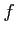 を1 対 1 写像(one-to-one mapping)または
単射(injection)という.
ただし
を1 対 1 写像(one-to-one mapping)または
単射(injection)という.
ただし 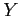 の元の中に対応づけがない元があってもよい.
の元の中に対応づけがない元があってもよい.
定義 2.9 (全単射)
写像 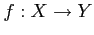 が全射かつ単射であれば,
が全射かつ単射であれば,
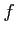 を上への 1 対 1 写像または
全単射(bijection)という.
を上への 1 対 1 写像または
全単射(bijection)という.
例 2.10 (写像の分類)
- 写像
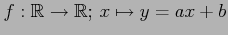 は全単射である.
は全単射である.
- 写像
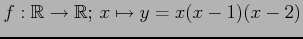 は全射である.
は全射である.
- 写像
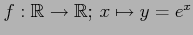 は単射である.
は単射である.
- 写像
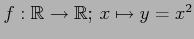 は
全射でも単射でもない.
は
全射でも単射でもない.
平成21年6月1日