2.1 写像
定義 2.1 (写像)
集合 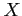 の各元に対して,
集合
の各元に対して,
集合 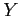 の元を対応させる規則
の元を対応させる規則 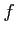 を
写像(mapping)といい,
を
写像(mapping)といい,
または
と表記する. さらには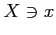 ,
, 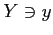 のとき
のとき
または
と表記する.
または
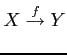 |
と表記する. さらには
または
と表記する.
注意 2.2 (写像)
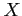 のすべての元に対して対応規則を定める.
のすべての元に対して対応規則を定める.
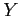 の元に対しては対応づけされていない元があってもよい.
また,
の元に対しては対応づけされていない元があってもよい.
また, 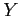 のあるひとつの元
のあるひとつの元 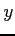 に対して
に対して 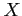 の複数の元
の複数の元
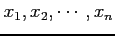 が対応づけされていてもよい.
が対応づけされていてもよい.
注意 2.3 (写像)
写像 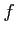 が
が 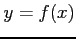 の形の式で表されるとき
の形の式で表されるとき 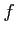 を
関数(function)とも呼ぶ.
を
関数(function)とも呼ぶ.
注意 2.4 (変換)
写像 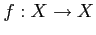 に対しては
に対しては 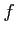 を変換(transformation)とも呼ぶ.
を変換(transformation)とも呼ぶ.
例 2.5 (写像の具体例)
集合
をとし,写像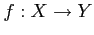 をひらがなをカタカナに対応させる規則とする.
このとき
をひらがなをカタカナに対応させる規則とする.
このとき
などが成り立つ.
をとし,写像
| ア |
などが成り立つ.
例 2.6 (写像の具体例)
関数
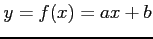 は
は
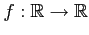 の写像である.
の写像である.
平成21年6月1日