6.6 演習 〜 不定積分,置換積分,部分積分
問 6.35 (不定積分)
次の不定積分を書け.
(1)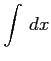 (2)
(2)
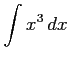 (3)
(3)
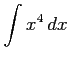 (4)
(4)
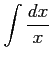 (5)
(5)
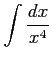 (6)
(6)
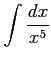 (7)
(7)
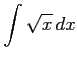
(8)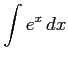 (9)
(9)
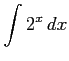 (10)
(10)
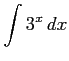 (11)
(11)
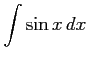 (12)
(12)
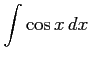 (13)
(13)
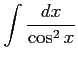
(14)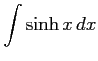 (15)
(15)
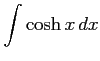 (16)
(16)
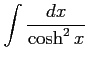 (17)
(17)
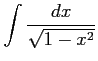 (18)
(18)
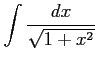
(19)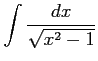 (20)
(20)
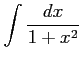 (21)
(21)
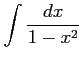
(1)
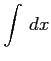 (2)
(2)
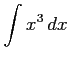 (3)
(3)
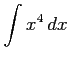 (4)
(4)
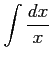 (5)
(5)
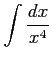 (6)
(6)
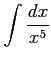 (7)
(7)
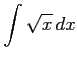
(8)
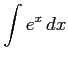 (9)
(9)
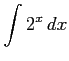 (10)
(10)
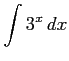 (11)
(11)
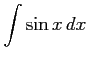 (12)
(12)
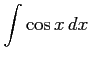 (13)
(13)
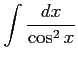
(14)
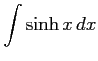 (15)
(15)
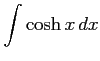 (16)
(16)
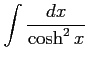 (17)
(17)
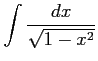 (18)
(18)
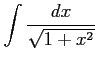
(19)
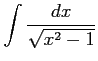 (20)
(20)
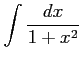 (21)
(21)
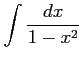
問 6.36 (不定積分の計算)
次の不定積分を求めよ.
(1)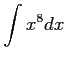 (2)
(2)
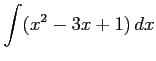 (3)
(3)
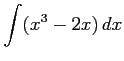 (4)
(4)
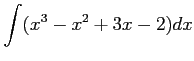
(5)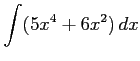 (6)
(6)
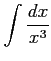 (7)
(7)
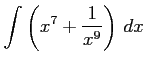 (8)
(8)
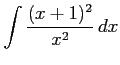 (9)
(9)
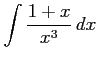
(10)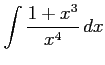 (11)
(11)
![$ \displaystyle{\int\sqrt[4]{x} dx}$](img2754.png) (12)
(12)
![$ \displaystyle{\int(1+x)\sqrt[3]{x}\,dx}$](img2755.png) (13)
(13)
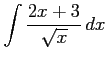
(14)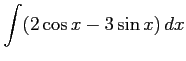 (15)
(15)
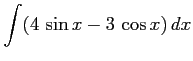 (16)
(16)
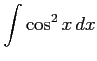 (倍角)
(倍角)
(1)
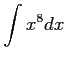 (2)
(2)
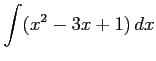 (3)
(3)
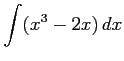 (4)
(4)
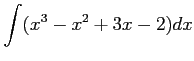
(5)
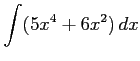 (6)
(6)
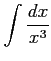 (7)
(7)
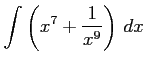 (8)
(8)
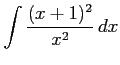 (9)
(9)
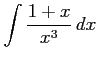
(10)
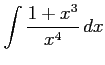 (11)
(11)
![$ \displaystyle{\int\sqrt[4]{x} dx}$](img2754.png) (12)
(12)
![$ \displaystyle{\int(1+x)\sqrt[3]{x}\,dx}$](img2755.png) (13)
(13)
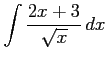
(14)
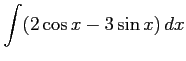 (15)
(15)
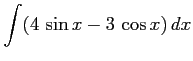 (16)
(16)
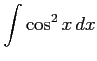 (倍角)
(倍角)
問 6.37 (置換積分法)
次の不定積分を求めよ.
(ヒント: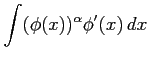 )
)
(1)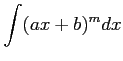 (2)
(2)
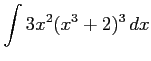 (3)
(3)
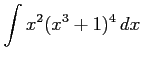 (4)
(4)
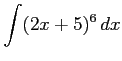
(5)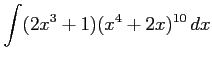 (6)
(6)
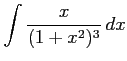 (7)
(7)
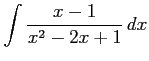 (8)
(8)
![$ \displaystyle{\int\sqrt[3]{1+x}\,\,dx}$](img2768.png)
(9)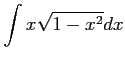 (10)
(10)
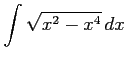 (11)
(11)
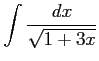 (12)
(12)
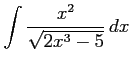
(13)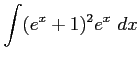 (14)
(14)
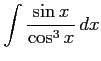 (15)
(15)
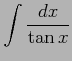 (16)
(16)
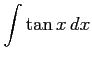
(17)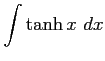 (18)
(18)
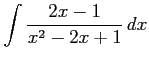 (2つに分ける)
(19)
(2つに分ける)
(19)
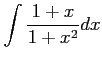 (2つに)
(2つに)
(ヒント:多項式)
(20)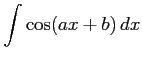 (
(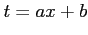 )
(21)
)
(21)
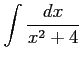 (
(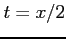 )
(22)
)
(22)
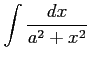 (
(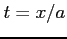 )
)
(23)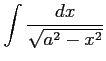 (24)
(24)
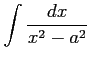 (25)
(25)
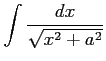 (26)
(26)
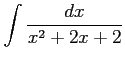 (
(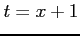 )
)
(27)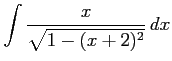 (
(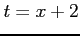 )
(28)
)
(28)
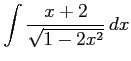 (2つに)
(2つに)
(29)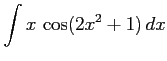 (
(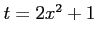 )
(30)
)
(30)
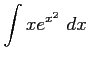 (
(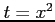 )
)
(31)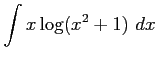 (
(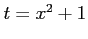 )
(32)
)
(32)
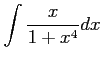 (
(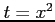 )
)
(33)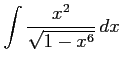 (
(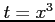 )
(34)
)
(34)
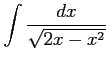 (
( )
)
(ヒント: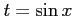 ,
, 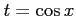 ,
, 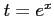 ,
, 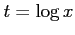 )
)
(35)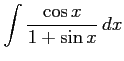 (36)
(36)
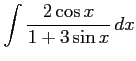 (37)
(37)
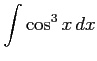 (
(
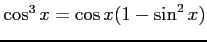 )
)
(38)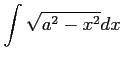 (
(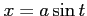 )
(39)
)
(39)
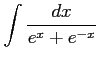 (40)
(40)
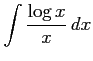 (41)
(41)
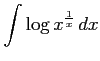
(42)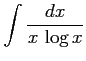
(ヒント:
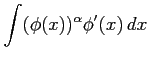 )
)
(1)
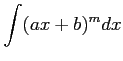 (2)
(2)
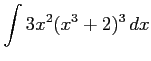 (3)
(3)
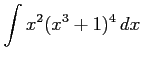 (4)
(4)
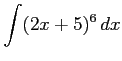
(5)
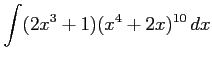 (6)
(6)
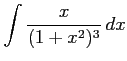 (7)
(7)
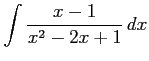 (8)
(8)
![$ \displaystyle{\int\sqrt[3]{1+x}\,\,dx}$](img2768.png)
(9)
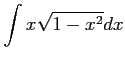 (10)
(10)
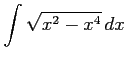 (11)
(11)
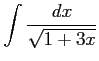 (12)
(12)
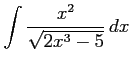
(13)
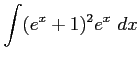 (14)
(14)
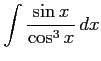 (15)
(15)
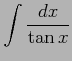 (16)
(16)
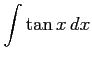
(17)
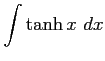 (18)
(18)
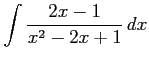 (2つに分ける)
(19)
(2つに分ける)
(19)
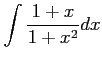 (2つに)
(2つに)
(ヒント:多項式)
(20)
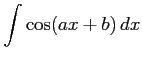 (
(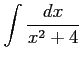 (
(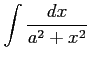 (
((23)
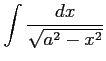 (24)
(24)
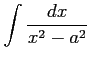 (25)
(25)
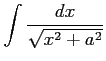 (26)
(26)
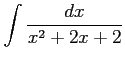 (
((27)
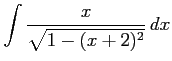 (
(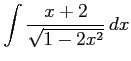 (2つに)
(2つに)
(29)
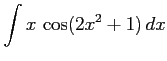 (
(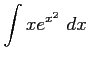 (
((31)
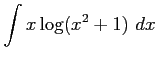 (
(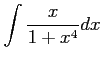 (
((33)
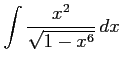 (
(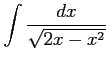 (
((ヒント:
(35)
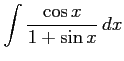 (36)
(36)
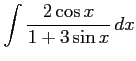 (37)
(37)
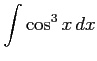 (
(
(38)
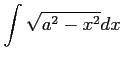 (
(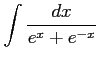 (40)
(40)
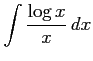 (41)
(41)
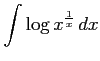
(42)
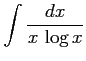
問 6.38 (部分積分法)
次の不定積分を求めよ.
(1)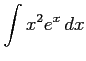 (2)
(2)
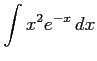 (3)
(3)
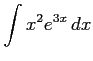 (4)
(4)
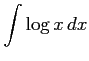 (5)
(5)
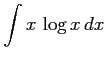
(6)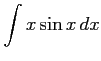 (7)
(7)
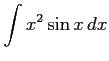 (8)
(8)
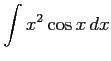 (9)
(9)
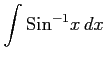 (10)
(10)
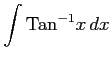
(11)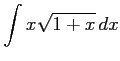 (12)
(12)
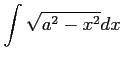 (13)
(13)
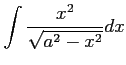
(1)
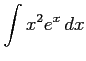 (2)
(2)
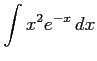 (3)
(3)
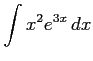 (4)
(4)
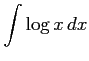 (5)
(5)
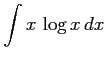
(6)
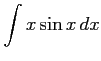 (7)
(7)
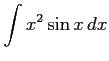 (8)
(8)
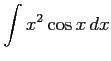 (9)
(9)
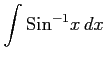 (10)
(10)
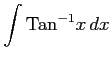
(11)
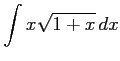 (12)
(12)
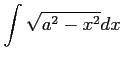 (13)
(13)
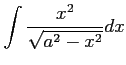
問 6.39 (部分積分法)
次の不定積分を求めよ.
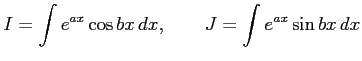 |
問 6.40 (部分積分法)
次の不定積分を求めよ.
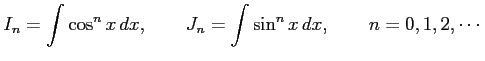 |
平成21年6月1日