5.7 べき関数のマクローリン級数
例 5.9 (多項式のテイラー級数)
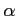 が自然数以外の実数のとき,
が自然数以外の実数のとき,
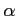 が自然数のとき,
が自然数のとき,
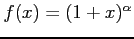 とおく.
導関数を計算すると
とおく.
導関数を計算すると
である.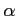 が自然数の場合と,
それ以外の場合に分けて考える.
まず
が自然数の場合と,
それ以外の場合に分けて考える.
まず 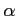 が自然数以外の実数のときを考える.
導関数は
が自然数以外の実数のときを考える.
導関数は
と表わされる. 点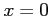 における微分係数は
における微分係数は
となる. よってテーラー級数は
と求まる. 収束半径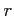 は
は
とおくと,
と得られる. 次に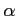 が自然数のときを考える.
導関数は
が自然数のときを考える.
導関数は
と表わされる. 点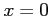 における微分係数は
における微分係数は
と求まる. よってテーラー級数は
と得られる. この展開式は有限項の和であり,有限次数の多項式である.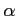 が自然数のときのテーラー展開は
二項展開となる.
展開式は多項式であり任意の実数
が自然数のときのテーラー展開は
二項展開となる.
展開式は多項式であり任意の実数 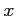 に対して成立する.
よって
に対して成立する.
よって
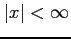 であり,収束半径は
であり,収束半径は 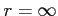 となる.
となる.
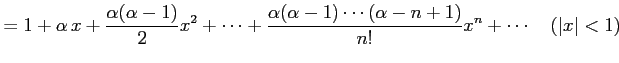 |
||
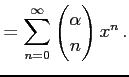 |
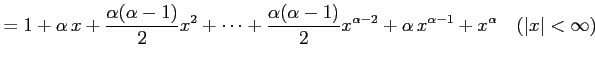 |
||
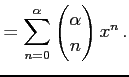 |
(導出)
である.
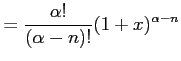 |
と表わされる. 点
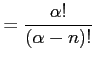 |
となる. よってテーラー級数は
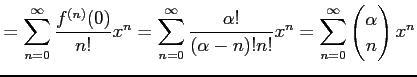 |
と求まる. 収束半径
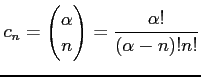 |
とおくと,
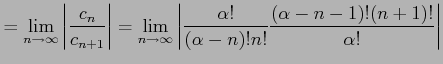 |
||
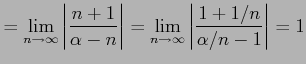 |
と得られる. 次に
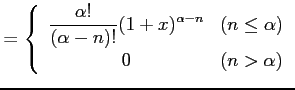 |
と表わされる. 点
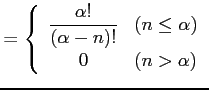 |
と求まる. よってテーラー級数は
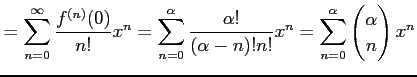 |
と得られる. この展開式は有限項の和であり,有限次数の多項式である.
平成21年6月1日