4.4 行列式の定義
定義 4.38 (行列式)
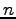 次正方行列
次正方行列
![$ A=[a_{ij}]_{m\times n}$](img1153.png) に対して
に対して
を の行列式(determinant)という.
の行列式(determinant)という.
 の行列式はまた
の行列式はまた
と書き表す.
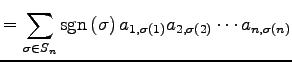 |
(673) |
を
 |
(674) |
と書き表す.
例 4.39 (行列式の具体例)
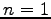 のとき,
のとき,
より,行列式は
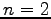 のとき,
のとき,
より, 行列式は
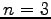 のとき,
のとき,
より,行列式は
| (675) |
より,行列式は
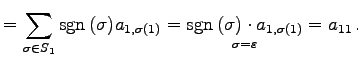 |
(676) |
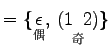 |
(677) |
より, 行列式は
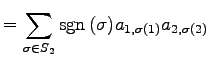 |
(678) | |
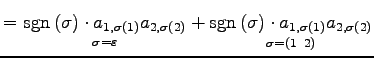 |
(679) | |
| (680) |
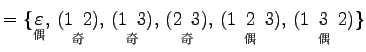 |
(681) |
より,行列式は
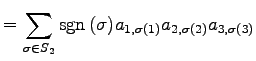 |
(682) | |
| (683) |
問 4.40 (行列式の具体例)
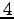 次の行列式を定義に従い書き下せ.
次の行列式を定義に従い書き下せ.
注意 4.41 (サルスの方法)
 次の行列式まではサルスの方法により
符合が簡単に定まる.
右斜め下向きの組合わせでは正をとり,
左斜め下向きの組合わせでは負となる.
次の行列式まではサルスの方法により
符合が簡単に定まる.
右斜め下向きの組合わせでは正をとり,
左斜め下向きの組合わせでは負となる.
 次以上の行列式ではこのルールは適用できない.
次以上の行列式ではこのルールは適用できない.
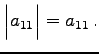 |
(684) | |
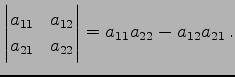 |
(685) | |
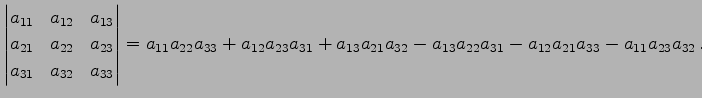 |
(686) |
注意 4.42 (行列式の計算)
置換 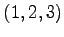 を一組ずつ互換をとると,
を一組ずつ互換をとると,
置換 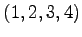 を一組ずつ互換をとると,
を一組ずつ互換をとると,
| 偶 | 奇 | 偶 | ||
|
|
|
|||
| |
|
|
||
| |
|
|
| 偶 | 奇 | 偶 | 奇 | |||
|
|
|
|||||
| |
|
|||||
| |
|
|||||
| |
|
|||||
| |
|
|||||
| |
|
|||||
| |
|
|
||||
| |
||||||
| |
|
|||||
| |
|
|
||||
| |
||||||
| |
|
平成20年2月2日