4.3 多項式の文字の置換
定義 4.30 (多項式の変数の置換)
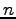 変数
変数 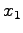 ,
, 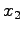 ,
,  ,
, 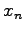 の
多項式
の
多項式
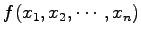 と
置換
と
置換
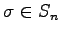 に対して
に対して
と定義する.
| (647) |
と定義する.
例 4.31 (多項式の変数の置換の具体例)
とする.
のとき
となる.
のとき
となる.
| (648) |
とする.
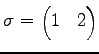 |
(649) |
のとき
| (650) |
となる.
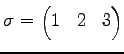 |
(651) |
のとき
| (652) |
となる.
定理 4.32 (置換の積)
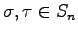 に対して
に対して
が成立する.
| (653) |
が成立する.
(証明)
| (左辺) | (654) | |
| (右辺) | (655) | |
| (656) |
定義 4.33 (差積)
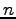 変数
変数
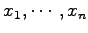 の多項式
の多項式
を差積と呼ぶ.
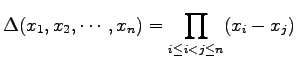 |
(657) |
を差積と呼ぶ.
例 4.34 (差積の具体例)
| (658) | ||
| (659) | ||
| (660) | ||
| (661) | ||
| (662) | ||
| (663) | ||
| (664) |
定理 4.35 (互換による差積の置換)
互換
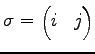 に対して
に対して
が成立する.
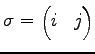 に対して
に対して
| (665) |
が成立する.
定理 4.36 (差積の変数の置換)
置換
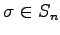 に対して
に対して
が成立する.
| (666) |
が成立する.
定理 4.37 (置換の符号の一意性)
置換の符合は互換の積の表わし方によらず一意に定まる.
とする. このときそれぞれ
となる.よって
である.恒等的には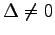 であるから
であるから
が成立する. 以上より符合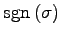 は互換の積の表し方によらず
は互換の積の表し方によらず
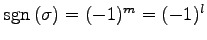 と一意に定まる.
と一意に定まる.
(証明)
置換 ![]() が互換の積を用いて二通りで表せたとする.
すなわち,
が互換の積を用いて二通りで表せたとする.
すなわち,
| (667) | ||
| (668) |
とする. このときそれぞれ
| (669) | |
| (670) |
となる.よって
| (671) |
である.恒等的には
| (672) |
が成立する. 以上より符合
平成20年2月2日