3.17 演習問題 〜 逆行列,行列の正則性
問 3.72 (逆行列)
次の行列の逆行列を求めよ.
ただし 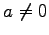 とする.
とする.
(1)![$ \begin{bmatrix}1\! & \!2 \\ [-0.5ex] 3\! & \!4 \end{bmatrix}$](img1842.png) (2)
(2)
![$ \begin{bmatrix}2\! & \!3 \\ [-0.5ex] 4\! & \!6 \end{bmatrix}$](img1843.png) (3)
(3)
![$ \begin{bmatrix}0\! & \!2 \\ [-0.5ex] 3\! & \!0 \end{bmatrix}$](img1844.png) (4)
(4)
![$ \begin{bmatrix}1\! & \!1\! & \!1 \\ [-0.5ex] 2\! & \!1\! & \!2 \\ [-0.5ex] 3\! & \!2\! & \!4 \end{bmatrix}$](img1845.png) (5)
(5)
![$ \begin{bmatrix}1\! & \!2\! & \!1 \\ [-0.5ex] 0\! & \!4\! & \!3 \\ [-0.5ex] 4\! & \!3\! & \!0 \end{bmatrix}$](img1846.png) (6)
(6)
![$ \begin{bmatrix}1\! & \!0\! & \!3 \\ [-0.5ex] 2\! & \!4\! & \!1 \\ [-0.5ex] 1\! & \!3\! & \!0 \end{bmatrix}$](img1847.png)
(7)![$ \begin{bmatrix}1\! & \!2\! & \!1 \\ [-0.5ex] 2\! & \!3\! & \!1 \\ [-0.5ex] 1\! & \!2\! & \!2 \end{bmatrix}$](img1848.png) (8)
(8)
![$ \begin{bmatrix}2\! & \!-1\! & \!0 \\ [-0.5ex] 2\! & \!-1\! & \!-1 \\ [-0.5ex] 1\! & \!0\! & \!-1 \end{bmatrix}$](img1849.png) (9)
(9)
![$ \begin{bmatrix}-3\! & \!-6\! & \!2 \\ [-0.5ex] 3\! & \!5\! & \!-2 \\ [-0.5ex] 1\! & \!3\! & \!-1 \end{bmatrix}$](img1850.png) (10)
(10)
![$ \begin{bmatrix}1\! & \!-1\! & \!-3 \\ [-0.5ex] 1\! & \!1\! & \!-1 \\ [-0.5ex] -1\! & \!1\! & \!5 \end{bmatrix}$](img1851.png) (11)
(11)
![$ \begin{bmatrix}1\! & \!0\! & \!1 \\ [-0.5ex] 2\! & \!2\! & \!3 \\ [-0.5ex] 1\! & \!-1\! & \!1 \end{bmatrix}$](img1852.png)
(12)![$ \begin{bmatrix}1\! & \!5\! & \!3 \\ [-0.5ex] 11\! & \!2\! & \!9 \\ [-0.5ex] 2\! & \!-1\! & \!1 \end{bmatrix}$](img1853.png) (13)
(13)
![$ \begin{bmatrix}a\! & \!1\! & \!1 \\ [-0.5ex] 0\! & \!a\! & \!1 \\ [-0.5ex] 0\! & \!0\! & \!a \end{bmatrix}$](img1854.png) (14)
(14)
![$ \begin{bmatrix}1\! & \!1\! & \!-a+1 \\ [-0.5ex] 2\! & \!3\! & \!2a \\ [-0.5ex] 1\! & \!1\! & \!1 \end{bmatrix}$](img1855.png) (15)
(15)
![$ \begin{bmatrix}2\! & \!1\! & \!4-a \\ [-0.5ex] 1\! & \!1\! & \!3 \\ [-0.5ex] a\! & \!1\! & \!2+a \end{bmatrix}$](img1856.png)
(16)![$ \begin{bmatrix}2\! & \!1\! & \!0 \\ [-0.5ex] 1\! & \!-1\! & 2 \\ [-0.5ex] -1\! & \!0\! & \!-1 \end{bmatrix}$](img1857.png) (17)
(17)
![$ \begin{bmatrix}1\! & \!0\! & \!-1\! & \!2 \\ [-0.5ex] 2\! & \!1\! & \!1\! & \!...
...\! & \!-1\! & \!-1\! & \!1 \\ [-0.5ex] 1\! & \!2\! & \!2\! & \!-2 \end{bmatrix}$](img1858.png) (18)
(18)
![$ \begin{bmatrix}1\! & \!1\! & \!1\! & \!1 \\ [-0.5ex] 0\! & \!1\! & \!1\! & \!1...
...] 0\! & \!0\! & \!1\! & \!1 \\ [-0.5ex] 0\! & \!0\! & \!0\! & \!1 \end{bmatrix}$](img1859.png) (19)
(19)
![$ \begin{bmatrix}2\! & \!0\! & \!1\! & \!0 \\ [-0.5ex] 0\! & \!-1\! & \!1\! & \!...
... 1\! & \!0\! & \!1\! & \!0 \\ [-0.5ex] 0\! & \!1\! & \!-1\! & \!3 \end{bmatrix}$](img1860.png)
(20)![$ \begin{bmatrix}0\! & \!1\! & \!0\! & \!0 \\ [-0.5ex] 1\! & \!1\! & \!1\! & \!1...
... -1\! & \!0\! & \!2\! & \!0 \\ [-0.5ex] 0\! & \!-2\! & \!1\! & \!0\end{bmatrix}$](img1861.png) (21)
(21)
![$ \begin{bmatrix}1\! & \!0\! & \!0\! & \!3\! & \!-1 \\ [-0.5ex] 0\! & \!1\! & \!...
...! & \!2\! & \!-4\! \\ [-0.5ex] 0\! & \!0\! & \!0\! & \!-1\! & \!3 \end{bmatrix}$](img1862.png)
(1)
![$ \begin{bmatrix}1\! & \!2 \\ [-0.5ex] 3\! & \!4 \end{bmatrix}$](img1842.png) (2)
(2)
![$ \begin{bmatrix}2\! & \!3 \\ [-0.5ex] 4\! & \!6 \end{bmatrix}$](img1843.png) (3)
(3)
![$ \begin{bmatrix}0\! & \!2 \\ [-0.5ex] 3\! & \!0 \end{bmatrix}$](img1844.png) (4)
(4)
![$ \begin{bmatrix}1\! & \!1\! & \!1 \\ [-0.5ex] 2\! & \!1\! & \!2 \\ [-0.5ex] 3\! & \!2\! & \!4 \end{bmatrix}$](img1845.png) (5)
(5)
![$ \begin{bmatrix}1\! & \!2\! & \!1 \\ [-0.5ex] 0\! & \!4\! & \!3 \\ [-0.5ex] 4\! & \!3\! & \!0 \end{bmatrix}$](img1846.png) (6)
(6)
![$ \begin{bmatrix}1\! & \!0\! & \!3 \\ [-0.5ex] 2\! & \!4\! & \!1 \\ [-0.5ex] 1\! & \!3\! & \!0 \end{bmatrix}$](img1847.png)
(7)
![$ \begin{bmatrix}1\! & \!2\! & \!1 \\ [-0.5ex] 2\! & \!3\! & \!1 \\ [-0.5ex] 1\! & \!2\! & \!2 \end{bmatrix}$](img1848.png) (8)
(8)
![$ \begin{bmatrix}2\! & \!-1\! & \!0 \\ [-0.5ex] 2\! & \!-1\! & \!-1 \\ [-0.5ex] 1\! & \!0\! & \!-1 \end{bmatrix}$](img1849.png) (9)
(9)
![$ \begin{bmatrix}-3\! & \!-6\! & \!2 \\ [-0.5ex] 3\! & \!5\! & \!-2 \\ [-0.5ex] 1\! & \!3\! & \!-1 \end{bmatrix}$](img1850.png) (10)
(10)
![$ \begin{bmatrix}1\! & \!-1\! & \!-3 \\ [-0.5ex] 1\! & \!1\! & \!-1 \\ [-0.5ex] -1\! & \!1\! & \!5 \end{bmatrix}$](img1851.png) (11)
(11)
![$ \begin{bmatrix}1\! & \!0\! & \!1 \\ [-0.5ex] 2\! & \!2\! & \!3 \\ [-0.5ex] 1\! & \!-1\! & \!1 \end{bmatrix}$](img1852.png)
(12)
![$ \begin{bmatrix}1\! & \!5\! & \!3 \\ [-0.5ex] 11\! & \!2\! & \!9 \\ [-0.5ex] 2\! & \!-1\! & \!1 \end{bmatrix}$](img1853.png) (13)
(13)
![$ \begin{bmatrix}a\! & \!1\! & \!1 \\ [-0.5ex] 0\! & \!a\! & \!1 \\ [-0.5ex] 0\! & \!0\! & \!a \end{bmatrix}$](img1854.png) (14)
(14)
![$ \begin{bmatrix}1\! & \!1\! & \!-a+1 \\ [-0.5ex] 2\! & \!3\! & \!2a \\ [-0.5ex] 1\! & \!1\! & \!1 \end{bmatrix}$](img1855.png) (15)
(15)
![$ \begin{bmatrix}2\! & \!1\! & \!4-a \\ [-0.5ex] 1\! & \!1\! & \!3 \\ [-0.5ex] a\! & \!1\! & \!2+a \end{bmatrix}$](img1856.png)
(16)
![$ \begin{bmatrix}2\! & \!1\! & \!0 \\ [-0.5ex] 1\! & \!-1\! & 2 \\ [-0.5ex] -1\! & \!0\! & \!-1 \end{bmatrix}$](img1857.png) (17)
(17)
![$ \begin{bmatrix}1\! & \!0\! & \!-1\! & \!2 \\ [-0.5ex] 2\! & \!1\! & \!1\! & \!...
...\! & \!-1\! & \!-1\! & \!1 \\ [-0.5ex] 1\! & \!2\! & \!2\! & \!-2 \end{bmatrix}$](img1858.png) (18)
(18)
![$ \begin{bmatrix}1\! & \!1\! & \!1\! & \!1 \\ [-0.5ex] 0\! & \!1\! & \!1\! & \!1...
...] 0\! & \!0\! & \!1\! & \!1 \\ [-0.5ex] 0\! & \!0\! & \!0\! & \!1 \end{bmatrix}$](img1859.png) (19)
(19)
![$ \begin{bmatrix}2\! & \!0\! & \!1\! & \!0 \\ [-0.5ex] 0\! & \!-1\! & \!1\! & \!...
... 1\! & \!0\! & \!1\! & \!0 \\ [-0.5ex] 0\! & \!1\! & \!-1\! & \!3 \end{bmatrix}$](img1860.png)
(20)
![$ \begin{bmatrix}0\! & \!1\! & \!0\! & \!0 \\ [-0.5ex] 1\! & \!1\! & \!1\! & \!1...
... -1\! & \!0\! & \!2\! & \!0 \\ [-0.5ex] 0\! & \!-2\! & \!1\! & \!0\end{bmatrix}$](img1861.png) (21)
(21)
![$ \begin{bmatrix}1\! & \!0\! & \!0\! & \!3\! & \!-1 \\ [-0.5ex] 0\! & \!1\! & \!...
...! & \!2\! & \!-4\! \\ [-0.5ex] 0\! & \!0\! & \!0\! & \!-1\! & \!3 \end{bmatrix}$](img1862.png)
問 3.73 (逆行列)
行列
![$ A=\begin{bmatrix}
0\! & \!1\! & \!1 \\ [-0.5ex] -1\! & \!0\! & \!1 \\ [-0.5ex] -1\!
& \!-1\! & \!0
\end{bmatrix}$](img1863.png) に対して,行列
に対して,行列
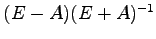 を求めよ.
を求めよ.
![$ A=\begin{bmatrix}
0\! & \!1\! & \!1 \\ [-0.5ex] -1\! & \!0\! & \!1 \\ [-0.5ex] -1\!
& \!-1\! & \!0
\end{bmatrix}$](img1863.png) に対して,行列
に対して,行列
問 3.74 (行列の可換性)
 ,
,  が可換ならば,次の行列の組も可換であることを示せ.
が可換ならば,次の行列の組も可換であることを示せ.
(1)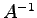 ,
,  (2)
(2) 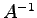 ,
, 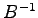 (3)
(3) 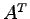 ,
, 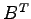
(1)
問 3.75 (行列の正則性)
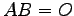 となる
となる 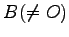 が存在するならば,
が存在するならば,  は正則でないことを示せ.
は正則でないことを示せ.
問 3.76 (行列の正則性)
次を示せ.
(1) が正則ならば,
が正則ならば,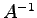 も正則で
も正則で
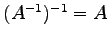 .
.
(2) が正則ならば,
が正則ならば,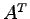 も正則で
も正則で
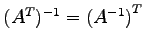 .
.
(3) ,
,  が正則ならば,
が正則ならば,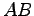 も正則で
も正則で
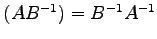 .
.
(1)
(2)
(3)
問 3.77 (正則行列)
 が巾零行列ならば
が巾零行列ならば 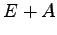 ,
, 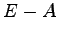 は共に正則行列であることを示せ.
また,その逆行列を求めよ.
は共に正則行列であることを示せ.
また,その逆行列を求めよ.
問 3.78 (正則行列)
次の等式をみたす行列  ,
,  を求めよ.
を求めよ.
(1)![$ \begin{bmatrix}
1\! & \!2 \\ [-0.5ex] 4\! & \!3
\end{bmatrix}A=
\begin{bmatrix}
0\! & \!8 \\ [-0.5ex] 1\! & \!2
\end{bmatrix}$](img1871.png) (2)
(2)
![$ B
\begin{bmatrix}
-1\! & \!-2 \\ [-0.5ex] 4\! & \!1
\end{bmatrix}=
\begin{bmatrix}
2\! & \!1 \\ [-0.5ex] -1\! & \!2
\end{bmatrix}$](img1872.png)
(1)
![$ \begin{bmatrix}
1\! & \!2 \\ [-0.5ex] 4\! & \!3
\end{bmatrix}A=
\begin{bmatrix}
0\! & \!8 \\ [-0.5ex] 1\! & \!2
\end{bmatrix}$](img1871.png) (2)
(2)
![$ B
\begin{bmatrix}
-1\! & \!-2 \\ [-0.5ex] 4\! & \!1
\end{bmatrix}=
\begin{bmatrix}
2\! & \!1 \\ [-0.5ex] -1\! & \!2
\end{bmatrix}$](img1872.png)
問 3.79 (対角化)
行列  ,
, 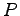 が次のとき
が次のとき 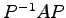 と
と
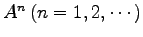 を求めよ.
を求めよ.
(1)![$ A=
\begin{bmatrix}
3\! & \!4 \\ [-0.5ex] -1\! & \!-2
\end{bmatrix}\quad P=
\begin{bmatrix}
4\! & \!1 \\ [-0.5ex] -1\! & \!-1
\end{bmatrix}$](img1875.png) (2)
(2)
![$ A=
\begin{bmatrix}
4\! & \!-3 \\ [-0.5ex] 2\! & \!-1
\end{bmatrix}\quad P=
\begin{bmatrix}
1\! & \!3 \\ [-0.5ex] 1\! & \!2
\end{bmatrix}$](img1876.png)
(1)
![$ A=
\begin{bmatrix}
3\! & \!4 \\ [-0.5ex] -1\! & \!-2
\end{bmatrix}\quad P=
\begin{bmatrix}
4\! & \!1 \\ [-0.5ex] -1\! & \!-1
\end{bmatrix}$](img1875.png) (2)
(2)
![$ A=
\begin{bmatrix}
4\! & \!-3 \\ [-0.5ex] 2\! & \!-1
\end{bmatrix}\quad P=
\begin{bmatrix}
1\! & \!3 \\ [-0.5ex] 1\! & \!2
\end{bmatrix}$](img1876.png)
平成20年2月2日