3.4 演習問題 〜 連立 1 次方程式,掃き出し法
問 3.15 (連立 1 次方程式)
次の連立 1 次方程式を行列を用いて表せ.
また連立 1 次方程式の係数行列,拡大係数行列を求めよ.
(1)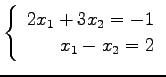 (2)
(2)
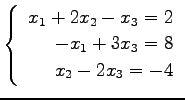 (3)
(3)
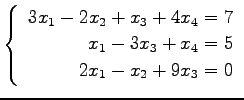
(1)
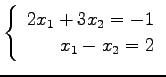 (2)
(2)
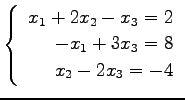 (3)
(3)
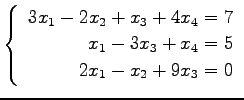
問 3.16 (掃き出し法)
次の連立 1 次方程式の解を求めよ.
ただし,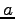 は実数とする.
は実数とする.
(1)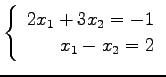 (2)
(2)
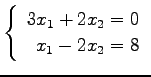 (3)
(3)
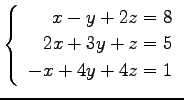
(4)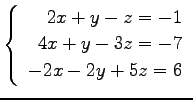 (5)
(5)
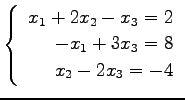 (6)
(6)
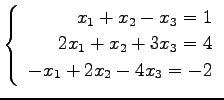
(7)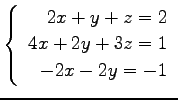 (8)
(8)
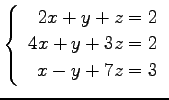 (9)
(9)
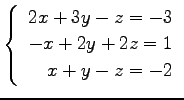
(10)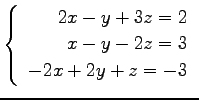 (11)
(11)
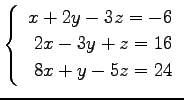 (12)
(12)
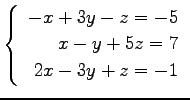
(13)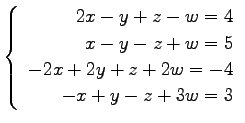 (14)
(14)
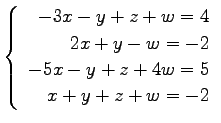 (15)
(15)
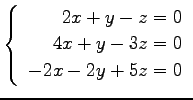
(16)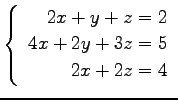 (17)
(17)
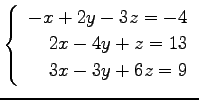 (18)
(18)
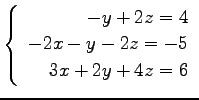
(19)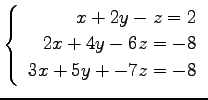 (20)
(20)
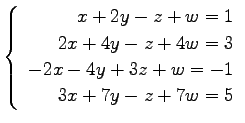
(21)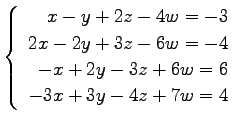 (22)
(22)
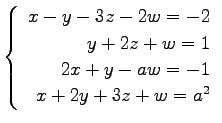
(1)
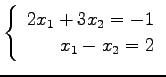 (2)
(2)
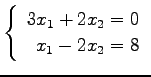 (3)
(3)
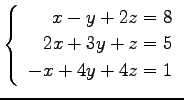
(4)
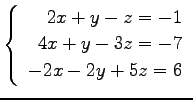 (5)
(5)
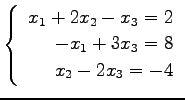 (6)
(6)
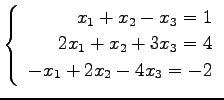
(7)
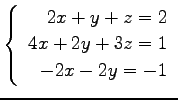 (8)
(8)
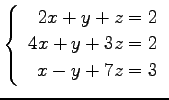 (9)
(9)
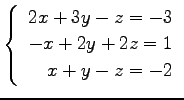
(10)
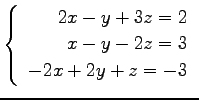 (11)
(11)
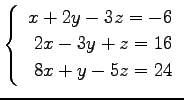 (12)
(12)
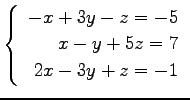
(13)
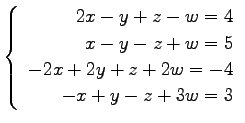 (14)
(14)
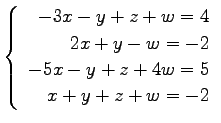 (15)
(15)
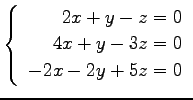
(16)
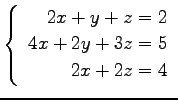 (17)
(17)
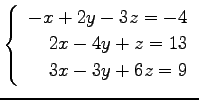 (18)
(18)
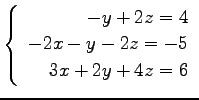
(19)
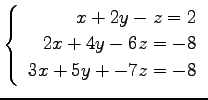 (20)
(20)
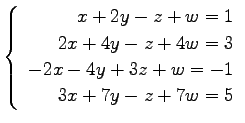
(21)
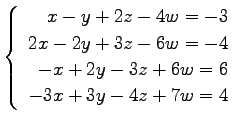 (22)
(22)
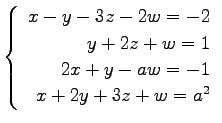
平成20年2月2日