2.19 演習問題 〜 行列の演算
問 2.77 (行列)
次の成分で与えられる
行列
![$ \displaystyle{\left[\,\,a_{i,j} \,\,\right]_{5\times 5}}$](img1279.png) を
具体的に書き下せ.
を
具体的に書き下せ.
(1)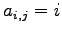 (2)
(2) 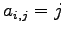 (3)
(3)
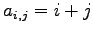 (4)
(4)
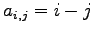 (5)
(5)
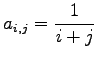
(6)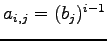 (7)
(7)
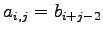 (8)
(8)
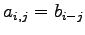 (9)
(9)
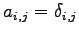 (10)
(10)
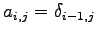
(11)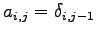 (12)
(12)
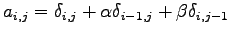
(1)
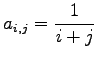
(6)
(11)
問 2.78 (行列のいろいろ)
次の行列のうち
零行列,正方行列,対角行列,単位行列,スカラー行列,
上三角行列,下三角行列,対称行列,交代行列(歪対称行列),
エルミート行列,歪エルミート行列,直交行列,ユニタリー行列
に当てはまる行列をすべてあげよ.
(1)![$ \begin{bmatrix}
0 \!&\! 0 \!&\! 0 \!&\! 0 \\ [-.5ex]
0 \!&\! 0 \!&\! 0 \!&\! 0...
...x]
0 \!&\! 0 \!&\! 0 \!&\! 0 \\ [-.5ex]
0 \!&\! 0 \!&\! 0 \!&\! 0
\end{bmatrix}$](img1292.png) (2)
(2)
![$ \begin{bmatrix}
1 \!&\! 0 \!&\! 0 \!&\! 0 \\ [-.5ex]
0 \!&\! 2 \!&\! 0 \!&\! 0...
...]
0 \!&\! 0 \!&\! -3 \!&\! 0 \\ [-.5ex]
0 \!&\! 0 \!&\! 0 \!&\! 3
\end{bmatrix}$](img1293.png) (3)
(3)
![$ \begin{bmatrix}
1 \!&\! 0 \!&\! 0 \!&\! 0 \\ [-.5ex]
0 \!&\! 1 \!&\! 0 \!&\! 0...
...x]
0 \!&\! 0 \!&\! 1 \!&\! 0 \\ [-.5ex]
0 \!&\! 0 \!&\! 0 \!&\! 1
\end{bmatrix}$](img1294.png) (4)
(4)
![$ \begin{bmatrix}
3 \!&\! 0 \!&\! 0 \!&\! 0 \\ [-.5ex]
0 \!&\! 3 \!&\! 0 \!&\! 0...
...x]
0 \!&\! 0 \!&\! 3 \!&\! 0 \\ [-.5ex]
0 \!&\! 0 \!&\! 0 \!&\! 3
\end{bmatrix}$](img1295.png) (5)
(5)
![$ \begin{bmatrix}
1 \!&\! 7 \!&\! 4 \!&\! 5 \\ [-.5ex]
0 \!&\! -1 \!&\! 2 \!&\! ...
...]
0 \!&\! 0 \!&\! 3 \!&\! -3 \\ [-.5ex]
0 \!&\! 0 \!&\! 0 \!&\! 3
\end{bmatrix}$](img1296.png)
(6)![$ \begin{bmatrix}
2 \!&\! 0 \!&\! 0 \!&\! 0 \\ [-.5ex]
3 \!&\! -2 \!&\! 0 \!&\! ...
...]
-1 \!&\! 7 \!&\! 4 \!&\! 0 \\ [-.5ex]
2 \!&\! 6 \!&\! 3 \!&\! 5
\end{bmatrix}$](img1297.png) (7)
(7)
![$ \begin{bmatrix}
2 \!&\! -4 \!&\! 7 \!&\! 1 \\ [-.5ex]
-4 \!&\! -2 \!&\! -3 \!&...
...]
7 \!&\! -3 \!&\! 3 \!&\! 9 \\ [-.5ex]
1 \!&\! 2 \!&\! 9 \!&\! 5
\end{bmatrix}$](img1298.png) (8)
(8)
![$ \begin{bmatrix}
0 \!&\! 1 \!&\! -2 \!&\! 3 \\ [-.5ex]
-1 \!&\! 0 \!&\! -5 \!&\...
...2 \!&\! 5 \!&\! 0 \!&\! -1 \\ [-.5ex]
-3 \!&\! -4 \!&\! 1 \!&\! 0
\end{bmatrix}$](img1299.png) (9)
(9)
![$ \begin{bmatrix}
\frac{1}{\sqrt{2}} \!&\! \frac{1}{\sqrt{2}} \\ [-.5ex]
\frac{1}{\sqrt{2}} \!&\! \frac{-1}{\sqrt{2}}
\end{bmatrix}$](img1300.png)
(10)![$ \begin{bmatrix}
1 \!&\! 1\!+\!i \!&\! -3\!+\!2i \!&\! 5i \\ [-.5ex]
1-i \!&\! ...
...&\! 7 \!&\! -1 \!&\! 8i \\ [-.5ex]
-5i \!&\! 3i \!&\! -8i \!&\! 3
\end{bmatrix}$](img1301.png) (11)
(11)
![$ \begin{bmatrix}
5i \!&\! 1\!+\!i \!&\! -3\!+\!2i \!&\! 5i \\ [-.5ex]
-1\!+\!i ...
...\!&\! 7 \!&\! 2i \!&\! -8 \\ [-.5ex]
5i \!&\! -3i \!&\! 8 \!&\! i
\end{bmatrix}$](img1302.png) (12)
(12)
![$ \begin{bmatrix}
\frac{i}{\sqrt{2}} \!&\! \frac{1}{\sqrt{2}} \\ [-.5ex]
\frac{1}{\sqrt{2}} \!&\! \frac{i}{\sqrt{2}}
\end{bmatrix}$](img1303.png)
(1)
![$ \begin{bmatrix}
0 \!&\! 0 \!&\! 0 \!&\! 0 \\ [-.5ex]
0 \!&\! 0 \!&\! 0 \!&\! 0...
...x]
0 \!&\! 0 \!&\! 0 \!&\! 0 \\ [-.5ex]
0 \!&\! 0 \!&\! 0 \!&\! 0
\end{bmatrix}$](img1292.png) (2)
(2)
![$ \begin{bmatrix}
1 \!&\! 0 \!&\! 0 \!&\! 0 \\ [-.5ex]
0 \!&\! 2 \!&\! 0 \!&\! 0...
...]
0 \!&\! 0 \!&\! -3 \!&\! 0 \\ [-.5ex]
0 \!&\! 0 \!&\! 0 \!&\! 3
\end{bmatrix}$](img1293.png) (3)
(3)
![$ \begin{bmatrix}
1 \!&\! 0 \!&\! 0 \!&\! 0 \\ [-.5ex]
0 \!&\! 1 \!&\! 0 \!&\! 0...
...x]
0 \!&\! 0 \!&\! 1 \!&\! 0 \\ [-.5ex]
0 \!&\! 0 \!&\! 0 \!&\! 1
\end{bmatrix}$](img1294.png) (4)
(4)
![$ \begin{bmatrix}
3 \!&\! 0 \!&\! 0 \!&\! 0 \\ [-.5ex]
0 \!&\! 3 \!&\! 0 \!&\! 0...
...x]
0 \!&\! 0 \!&\! 3 \!&\! 0 \\ [-.5ex]
0 \!&\! 0 \!&\! 0 \!&\! 3
\end{bmatrix}$](img1295.png) (5)
(5)
![$ \begin{bmatrix}
1 \!&\! 7 \!&\! 4 \!&\! 5 \\ [-.5ex]
0 \!&\! -1 \!&\! 2 \!&\! ...
...]
0 \!&\! 0 \!&\! 3 \!&\! -3 \\ [-.5ex]
0 \!&\! 0 \!&\! 0 \!&\! 3
\end{bmatrix}$](img1296.png)
(6)
![$ \begin{bmatrix}
2 \!&\! 0 \!&\! 0 \!&\! 0 \\ [-.5ex]
3 \!&\! -2 \!&\! 0 \!&\! ...
...]
-1 \!&\! 7 \!&\! 4 \!&\! 0 \\ [-.5ex]
2 \!&\! 6 \!&\! 3 \!&\! 5
\end{bmatrix}$](img1297.png) (7)
(7)
![$ \begin{bmatrix}
2 \!&\! -4 \!&\! 7 \!&\! 1 \\ [-.5ex]
-4 \!&\! -2 \!&\! -3 \!&...
...]
7 \!&\! -3 \!&\! 3 \!&\! 9 \\ [-.5ex]
1 \!&\! 2 \!&\! 9 \!&\! 5
\end{bmatrix}$](img1298.png) (8)
(8)
![$ \begin{bmatrix}
0 \!&\! 1 \!&\! -2 \!&\! 3 \\ [-.5ex]
-1 \!&\! 0 \!&\! -5 \!&\...
...2 \!&\! 5 \!&\! 0 \!&\! -1 \\ [-.5ex]
-3 \!&\! -4 \!&\! 1 \!&\! 0
\end{bmatrix}$](img1299.png) (9)
(9)
![$ \begin{bmatrix}
\frac{1}{\sqrt{2}} \!&\! \frac{1}{\sqrt{2}} \\ [-.5ex]
\frac{1}{\sqrt{2}} \!&\! \frac{-1}{\sqrt{2}}
\end{bmatrix}$](img1300.png)
(10)
![$ \begin{bmatrix}
1 \!&\! 1\!+\!i \!&\! -3\!+\!2i \!&\! 5i \\ [-.5ex]
1-i \!&\! ...
...&\! 7 \!&\! -1 \!&\! 8i \\ [-.5ex]
-5i \!&\! 3i \!&\! -8i \!&\! 3
\end{bmatrix}$](img1301.png) (11)
(11)
![$ \begin{bmatrix}
5i \!&\! 1\!+\!i \!&\! -3\!+\!2i \!&\! 5i \\ [-.5ex]
-1\!+\!i ...
...\!&\! 7 \!&\! 2i \!&\! -8 \\ [-.5ex]
5i \!&\! -3i \!&\! 8 \!&\! i
\end{bmatrix}$](img1302.png) (12)
(12)
![$ \begin{bmatrix}
\frac{i}{\sqrt{2}} \!&\! \frac{1}{\sqrt{2}} \\ [-.5ex]
\frac{1}{\sqrt{2}} \!&\! \frac{i}{\sqrt{2}}
\end{bmatrix}$](img1303.png)
問 2.79 (行列の演算)
次の関係式を証明せよ.
ただし,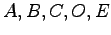 はそれぞれにおいて演算が定義可能な
型の行列とする.
はそれぞれにおいて演算が定義可能な
型の行列とする.
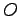 は零行列,
は零行列,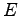 は単位行列,
は単位行列,
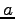 ,
, 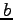 はスカラーとする.
はスカラーとする.
(1)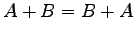 (2)
(2) 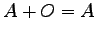 ,
, 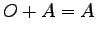 (3)
(3)
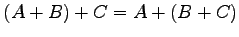
(4)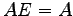 ,
, 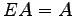 (5)
(5) 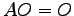 ,
, 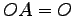 (6)
(6)
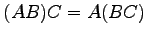
(7)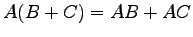 ,
,
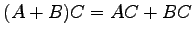 (8)
(8) 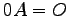 ,
, 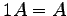
(9)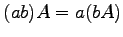 ,
,
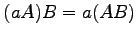 (10)
(10)
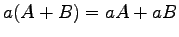 ,
,
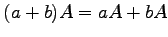
(11)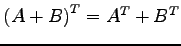 (12)
(12)
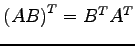 (13)
(13)
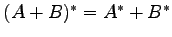
(14)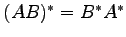
(1)
(4)
(7)
(9)
(11)
(14)
問 2.80 (行列の演算)
![$ A=
\begin{bmatrix}
2\! & \!-5\! & \!1 \\ [-0.5ex] 3\! & \!0\! & \!-4
\end{bmatrix}$](img1305.png) ,
,
![$ B=
\begin{bmatrix}
1\! & \!-2\! & \!-3 \\ [-0.5ex] 0\! & \!-1\! & \!5
\end{bmatrix}$](img1306.png) ,
,
![$ C=
\begin{bmatrix}
0\! & \!1\! & \!-2 \\ [-0.5ex] 1\! & \!-1\! & \!-1
\end{bmatrix}$](img1307.png) に対して,
に対して,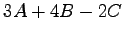 を求めよ.
を求めよ.
![$ A=
\begin{bmatrix}
2\! & \!-5\! & \!1 \\ [-0.5ex] 3\! & \!0\! & \!-4
\end{bmatrix}$](img1305.png) ,
,
![$ B=
\begin{bmatrix}
1\! & \!-2\! & \!-3 \\ [-0.5ex] 0\! & \!-1\! & \!5
\end{bmatrix}$](img1306.png) ,
,
![$ C=
\begin{bmatrix}
0\! & \!1\! & \!-2 \\ [-0.5ex] 1\! & \!-1\! & \!-1
\end{bmatrix}$](img1307.png) に対して,
に対して,
問 2.81 (行列の演算)
![$ A=
\begin{bmatrix}
1\! & \!-\!2 \\ [-0.5ex] \!-\!3\! & \!4
\end{bmatrix}$](img1309.png) ,
,
![$ B=
\begin{bmatrix}
5\! & \!3 \\ [-0.5ex] 2\! & \!-\!1
\end{bmatrix}$](img1310.png) ,
,
![$ C=
\begin{bmatrix}
6\! & \!4 \\ [-0.5ex] 3\! & \!5
\end{bmatrix}$](img1311.png) に対して,次を求めよ.
に対して,次を求めよ.
(1)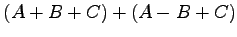 (2)
(2)
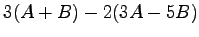
![$ A=
\begin{bmatrix}
1\! & \!-\!2 \\ [-0.5ex] \!-\!3\! & \!4
\end{bmatrix}$](img1309.png) ,
,
![$ B=
\begin{bmatrix}
5\! & \!3 \\ [-0.5ex] 2\! & \!-\!1
\end{bmatrix}$](img1310.png) ,
,
![$ C=
\begin{bmatrix}
6\! & \!4 \\ [-0.5ex] 3\! & \!5
\end{bmatrix}$](img1311.png) に対して,次を求めよ.
に対して,次を求めよ.
(1)
問 2.82 (行列の演算)
![$ A=
\begin{bmatrix}
1\! & \!0 \\ [-0.5ex] 2\! & \!1
\end{bmatrix}$](img1314.png) ,
,
![$ B=
\begin{bmatrix}
2\! & \!1 \\ [-0.5ex] -1\! & \!2
\end{bmatrix}$](img1315.png) に対して,次を計算せよ.
に対して,次を計算せよ.
(1)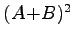 (2)
(2)
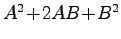 (3)
(3)
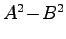 (4)
(4)
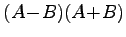 (5)
(5)
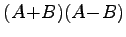
![$ A=
\begin{bmatrix}
1\! & \!0 \\ [-0.5ex] 2\! & \!1
\end{bmatrix}$](img1314.png) ,
,
![$ B=
\begin{bmatrix}
2\! & \!1 \\ [-0.5ex] -1\! & \!2
\end{bmatrix}$](img1315.png) に対して,次を計算せよ.
に対して,次を計算せよ.
(1)
問 2.83 (行列の演算)
![$ A=
\begin{bmatrix}
1\! & \!2 \\ [-0.5ex] 4\! & \!-3
\end{bmatrix}$](img1321.png) に対して,
に対して,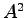 ,
,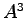 ,
,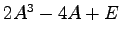 を求めよ.
を求めよ.
![$ A=
\begin{bmatrix}
1\! & \!2 \\ [-0.5ex] 4\! & \!-3
\end{bmatrix}$](img1321.png) に対して,
に対して,
問 2.84 (行列の演算)
行列  ,
,  ,
, 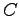 ,
, 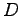 に対して,次の演算が可能ならば計算をせよ.
に対して,次の演算が可能ならば計算をせよ.
(1)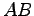 (2)
(2) 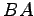 (3)
(3) 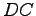 (4)
(4) 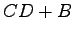 (5)
(5) 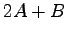 (6)
(6) 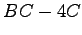 (7)
(7) 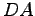
(8)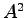 (9)
(9) 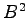 (10)
(10) 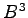
![$\displaystyle A= \begin{bmatrix}1\! & \!2 \\ [-0.5ex] 0\! & \!1 \\ [-0.5ex] 1\!...
...0.5ex] 0 \end{bmatrix}, \quad D= \begin{bmatrix}0\! & \!1\! & \!0 \end{bmatrix}$](img1325.png) |
(1)
(8)
問 2.85 (行列の演算)
行列
![$ A=
\begin{bmatrix}
1\! & \!2\! & \!0 \\ [-0.5ex] 3\! & \!-1\! & \!4
\end{bmatrix}$](img1334.png) のとき
のとき 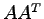 ,
, 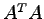 を求めよ.
を求めよ.
![$ A=
\begin{bmatrix}
1\! & \!2\! & \!0 \\ [-0.5ex] 3\! & \!-1\! & \!4
\end{bmatrix}$](img1334.png) のとき
のとき
問 2.86 (行列の演算)
行列  ,
,  ,
, 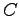 ,
, 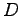 に対して,次の演算が可能ならば計算をせよ.
に対して,次の演算が可能ならば計算をせよ.
(1)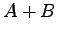 (2)
(2) 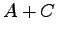 (3)
(3) 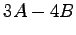 (4)
(4) 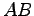 (5)
(5) 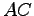 (6)
(6) 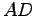 (7)
(7) 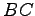
(8)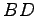 (9)
(9) 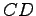 (10)
(10) 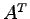 (11)
(11) 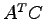 (12)
(12)
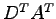 (13)
(13) 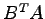 (14)
(14) 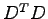
![$\displaystyle A= \begin{bmatrix}1\! & \!-1\! & \!2 \\ [-0.5ex] 0\! & \!3\! & \!...
...d{bmatrix},\quad D= \begin{bmatrix}2 \\ [-0.5ex] -1 \\ [-0.5ex] 3 \end{bmatrix}$](img1337.png) |
(1)
(8)
問 2.87 (行列の演算)
次の計算をせよ.
(1)![$ 3
\begin{bmatrix}
2 \\ [-0.5ex] -7 \\ [-0.5ex] 1
\end{bmatrix}$](img1347.png)
![$ -5
\begin{bmatrix}
-1 \\ [-0.5ex] 4 \\ [-0.5ex] -2
\end{bmatrix}$](img1348.png) (2)
(2)
![$ \begin{bmatrix}
2\! & \!3 \\ [-0.5ex] -1\! & \!4
\end{bmatrix}$](img1349.png)
![$ \begin{bmatrix}
3 \\ [-0.5ex] 1
\end{bmatrix}$](img1350.png) (3)
(3)
![$ \begin{bmatrix}
2\! & \!-1 \\ [-0.5ex] 7\! & \!6
\end{bmatrix}$](img1351.png)
![$ \begin{bmatrix}
3 \\ [-0.5ex] -5
\end{bmatrix}$](img1352.png) (4)
(4)
![$ \begin{bmatrix}
2\! & \!3 \\ [-0.5ex] -1\! & \!4
\end{bmatrix}$](img1349.png)
![$ \begin{bmatrix}
-3\! & \!4 \\ [-0.5ex] 1\! & \!1
\end{bmatrix}$](img1353.png)
(5)![$ \begin{bmatrix}
2\! & \!-3 \\ [-0.5ex] 1\! & \!4
\end{bmatrix}$](img1354.png)
![$ \begin{bmatrix}
-1\! & \!0 \\ [-0.5ex] 2\! & \!5
\end{bmatrix}$](img1355.png) (6)
(6)
![$ \begin{bmatrix}
2\! & \!1 \\ [-0.5ex] 1\! & \!3 \\ [-0.5ex] 1\! & \!-1
\end{bmatrix}$](img1356.png)
![$ \begin{bmatrix}
1\! & \!-1\! & \!2 \\ [-0.5ex] 1\! & \!2\! & \!3
\end{bmatrix}$](img1357.png) (7)
(7)
![$ \begin{bmatrix}
4\! & \!-1\! & \!5 \\ [-0.5ex] 0\! & \!1\! & \!2 \\ [-0.5ex] 2\! & \!-1\! & \!0
\end{bmatrix}$](img1358.png)
![$ \begin{bmatrix}
2 \\ [-0.5ex] 1 \\ [-0.5ex] -1
\end{bmatrix}$](img1359.png)
(8)![$ \begin{bmatrix}
1\! & \!2\! & \!-3 \\ [-0.5ex] 2\! & \!-3\! & \!1 \\ [-0.5ex] 8\! & \!1\! & \!-5
\end{bmatrix}$](img1360.png)
![$ \begin{bmatrix}
1 \\ [-0.5ex] 2 \\ [-0.5ex] 3
\end{bmatrix}$](img1361.png) (9)
(9)
![$ \begin{bmatrix}
-1\! & \!2\! & \!1 \\ [-0.5ex] 3\! & \!2\! & \!1
\end{bmatrix}$](img1362.png)
![$ \begin{bmatrix}
4\! & \!-1\! & \!1 \\ [-0.5ex] 2\! & \!2\! & \!-3 \\ [-0.5ex] 1\! & \!1\! & \!0
\end{bmatrix}$](img1363.png) (10)
(10)
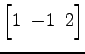
![$ \begin{bmatrix}
3\! & \!0\! & \!1 \\ [-0.5ex] 2\! & \!4\! & \!-1 \\ [-0.5ex] 1\! & \!-1\! & \!4
\end{bmatrix}$](img1365.png)
(11)![$ \begin{bmatrix}
1\! & \!3 \\ [-0.5ex] -2\! & \!1 \\ [-0.5ex] 5\! & \!-4 \\ [-0.5ex] -3\! & \!1
\end{bmatrix}$](img1366.png)
![$ \begin{bmatrix}
1\! & \!-1\! & \!4 \\ [-0.5ex] -2\! & \!1\! & \!-1
\end{bmatrix}$](img1367.png) (12)
(12)
![$ \begin{bmatrix}
2\! & \!i \\ [-0.5ex] -i\! & \!3
\end{bmatrix}$](img1368.png)
![$ \begin{bmatrix}
2-i\! & \!i \\ [-0.5ex] 0\! & \!1+i
\end{bmatrix}$](img1369.png)
(1)
![$ 3
\begin{bmatrix}
2 \\ [-0.5ex] -7 \\ [-0.5ex] 1
\end{bmatrix}$](img1347.png)
![$ -5
\begin{bmatrix}
-1 \\ [-0.5ex] 4 \\ [-0.5ex] -2
\end{bmatrix}$](img1348.png) (2)
(2)
![$ \begin{bmatrix}
2\! & \!3 \\ [-0.5ex] -1\! & \!4
\end{bmatrix}$](img1349.png)
![$ \begin{bmatrix}
2\! & \!-1 \\ [-0.5ex] 7\! & \!6
\end{bmatrix}$](img1351.png)
![$ \begin{bmatrix}
2\! & \!3 \\ [-0.5ex] -1\! & \!4
\end{bmatrix}$](img1349.png)
![$ \begin{bmatrix}
-3\! & \!4 \\ [-0.5ex] 1\! & \!1
\end{bmatrix}$](img1353.png)
(5)
![$ \begin{bmatrix}
2\! & \!-3 \\ [-0.5ex] 1\! & \!4
\end{bmatrix}$](img1354.png)
![$ \begin{bmatrix}
-1\! & \!0 \\ [-0.5ex] 2\! & \!5
\end{bmatrix}$](img1355.png) (6)
(6)
![$ \begin{bmatrix}
2\! & \!1 \\ [-0.5ex] 1\! & \!3 \\ [-0.5ex] 1\! & \!-1
\end{bmatrix}$](img1356.png)
![$ \begin{bmatrix}
1\! & \!-1\! & \!2 \\ [-0.5ex] 1\! & \!2\! & \!3
\end{bmatrix}$](img1357.png) (7)
(7)
![$ \begin{bmatrix}
4\! & \!-1\! & \!5 \\ [-0.5ex] 0\! & \!1\! & \!2 \\ [-0.5ex] 2\! & \!-1\! & \!0
\end{bmatrix}$](img1358.png)
![$ \begin{bmatrix}
2 \\ [-0.5ex] 1 \\ [-0.5ex] -1
\end{bmatrix}$](img1359.png)
(8)
![$ \begin{bmatrix}
1\! & \!2\! & \!-3 \\ [-0.5ex] 2\! & \!-3\! & \!1 \\ [-0.5ex] 8\! & \!1\! & \!-5
\end{bmatrix}$](img1360.png)
![$ \begin{bmatrix}
-1\! & \!2\! & \!1 \\ [-0.5ex] 3\! & \!2\! & \!1
\end{bmatrix}$](img1362.png)
![$ \begin{bmatrix}
4\! & \!-1\! & \!1 \\ [-0.5ex] 2\! & \!2\! & \!-3 \\ [-0.5ex] 1\! & \!1\! & \!0
\end{bmatrix}$](img1363.png) (10)
(10)
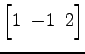
![$ \begin{bmatrix}
3\! & \!0\! & \!1 \\ [-0.5ex] 2\! & \!4\! & \!-1 \\ [-0.5ex] 1\! & \!-1\! & \!4
\end{bmatrix}$](img1365.png)
(11)
![$ \begin{bmatrix}
1\! & \!3 \\ [-0.5ex] -2\! & \!1 \\ [-0.5ex] 5\! & \!-4 \\ [-0.5ex] -3\! & \!1
\end{bmatrix}$](img1366.png)
![$ \begin{bmatrix}
1\! & \!-1\! & \!4 \\ [-0.5ex] -2\! & \!1\! & \!-1
\end{bmatrix}$](img1367.png) (12)
(12)
![$ \begin{bmatrix}
2\! & \!i \\ [-0.5ex] -i\! & \!3
\end{bmatrix}$](img1368.png)
![$ \begin{bmatrix}
2-i\! & \!i \\ [-0.5ex] 0\! & \!1+i
\end{bmatrix}$](img1369.png)
問 2.88 (巾行列)
次の巾行列を求めよ.ただし,
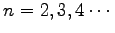 とする.
とする.
(1)![$ \begin{bmatrix}
a\! & \!b \\ [-0.5ex] c\! & \!-a
\end{bmatrix}^2$](img1371.png) (2)
(2)
![$ \begin{bmatrix}
0\! & \!-\!1 \\ [-0.5ex] 1\! & \!0
\end{bmatrix}^2$](img1372.png) (3)
(3)
![$ \begin{bmatrix}
1\! & \!1\! & \!-\!1 \\ [-0.5ex] 2\! & \!-\!1\! & \!0 \\ [-0.5ex] 1\! & \!-\!2\! & \!1
\end{bmatrix}^3$](img1373.png) (4)
(4)
![$ \begin{bmatrix}
1\! & \!2 \\ [-0.5ex] 0\! & \!1
\end{bmatrix}^n$](img1374.png) (5)
(5)
![$ \begin{bmatrix}
1\! & \!1\! & \!0 \\ [-0.5ex] 0\! & \!1\! & \!1 \\ [-0.5ex] 0\! & \!0\! & \!1
\end{bmatrix}^n$](img1375.png) (6)
(6)
![$ \begin{bmatrix}
0\! & \!0\! & \!-\!1\! & \!0 \\ [-0.5ex]
0\! & \!0\! & \!0\! ...
...\! & \!0\! & \!0\! & \!0 \\ [-0.5ex]
0\! & \!1\! & \!0\! & \!0
\end{bmatrix}^n$](img1376.png)
(1)
![$ \begin{bmatrix}
a\! & \!b \\ [-0.5ex] c\! & \!-a
\end{bmatrix}^2$](img1371.png) (2)
(2)
![$ \begin{bmatrix}
0\! & \!-\!1 \\ [-0.5ex] 1\! & \!0
\end{bmatrix}^2$](img1372.png) (3)
(3)
![$ \begin{bmatrix}
1\! & \!1\! & \!-\!1 \\ [-0.5ex] 2\! & \!-\!1\! & \!0 \\ [-0.5ex] 1\! & \!-\!2\! & \!1
\end{bmatrix}^3$](img1373.png) (4)
(4)
![$ \begin{bmatrix}
1\! & \!2 \\ [-0.5ex] 0\! & \!1
\end{bmatrix}^n$](img1374.png) (5)
(5)
![$ \begin{bmatrix}
1\! & \!1\! & \!0 \\ [-0.5ex] 0\! & \!1\! & \!1 \\ [-0.5ex] 0\! & \!0\! & \!1
\end{bmatrix}^n$](img1375.png) (6)
(6)
![$ \begin{bmatrix}
0\! & \!0\! & \!-\!1\! & \!0 \\ [-0.5ex]
0\! & \!0\! & \!0\! ...
...\! & \!0\! & \!0\! & \!0 \\ [-0.5ex]
0\! & \!1\! & \!0\! & \!0
\end{bmatrix}^n$](img1376.png)
問 2.89 (行列の演算)
次の関係式をみたす行列 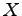 を求めよ.
を求めよ.
(1)![$ A=\begin{bmatrix}
2\! & \!-3 \\ [-0.5ex] 4\! & \!5
\end{bmatrix}$](img1377.png) ,
,
![$ B=\begin{bmatrix}
-5\! & \!2 \\ [-0.5ex] 3\! & \!7
\end{bmatrix}$](img1378.png) ,
,
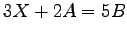
(2)![$ A=\begin{bmatrix}
1\! & \!2 \\ [-0.5ex] 3\! & \!4 \\ [-0.5ex] 5\! & \!0
\end{bmatrix}$](img1380.png) ,
,
![$ B=\begin{bmatrix}
-3\! & \!-2 \\ [-0.5ex] 1\! & \!-5 \\ [-0.5ex] 4\! & \!3
\end{bmatrix}$](img1381.png) ,
,
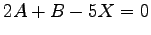
(3)![$ A=\begin{bmatrix}
-1\! & \!1\! & \!1 \\ [-0.5ex] 2\! & \!0\! & \!3
\end{bmatrix}$](img1383.png) ,
,
![$ B=\begin{bmatrix}
5\! & \!3\! & \!5 \\ [-0.5ex] 4\! & \!4\! & \!9
\end{bmatrix}$](img1384.png) ,
,
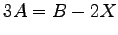
(1)
![$ A=\begin{bmatrix}
2\! & \!-3 \\ [-0.5ex] 4\! & \!5
\end{bmatrix}$](img1377.png) ,
,
![$ B=\begin{bmatrix}
-5\! & \!2 \\ [-0.5ex] 3\! & \!7
\end{bmatrix}$](img1378.png) ,
,
(2)
![$ A=\begin{bmatrix}
1\! & \!2 \\ [-0.5ex] 3\! & \!4 \\ [-0.5ex] 5\! & \!0
\end{bmatrix}$](img1380.png) ,
,
![$ B=\begin{bmatrix}
-3\! & \!-2 \\ [-0.5ex] 1\! & \!-5 \\ [-0.5ex] 4\! & \!3
\end{bmatrix}$](img1381.png) ,
,
(3)
![$ A=\begin{bmatrix}
-1\! & \!1\! & \!1 \\ [-0.5ex] 2\! & \!0\! & \!3
\end{bmatrix}$](img1383.png) ,
,
![$ B=\begin{bmatrix}
5\! & \!3\! & \!5 \\ [-0.5ex] 4\! & \!4\! & \!9
\end{bmatrix}$](img1384.png) ,
,
問 2.90 (行列の演算)
![$ 3
\begin{bmatrix}
x\! & \!y \\ [-0.5ex] z\! & \!w
\end{bmatrix}$](img1386.png) =
=
![$ \begin{bmatrix}
x\! & \!6 \\ [-0.5ex] -1\! & \!2w
\end{bmatrix}$](img1387.png) +
+
![$ \begin{bmatrix}
4\! & \!x+y \\ [-0.5ex] z+w\! & \!3
\end{bmatrix}$](img1388.png) をみたす
をみたす 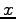 ,
, 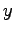 ,
, 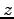 ,
, 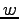 を求めよ.
を求めよ.
![$ 3
\begin{bmatrix}
x\! & \!y \\ [-0.5ex] z\! & \!w
\end{bmatrix}$](img1386.png) =
=
![$ \begin{bmatrix}
x\! & \!6 \\ [-0.5ex] -1\! & \!2w
\end{bmatrix}$](img1387.png) +
+
![$ \begin{bmatrix}
4\! & \!x+y \\ [-0.5ex] z+w\! & \!3
\end{bmatrix}$](img1388.png) をみたす
をみたす
問 2.91 (行列の演算)
![$ \begin{bmatrix}
0\! & \!c\! & \!b \\ [-0.5ex] c\! & \!0\! & \!a \\ [-0.5ex] b\...
...] ab\! & \!c^2+a^2\! & \!bc \\ [-0.5ex] ca\! & \!bc\! & \!a^2+b^2
\end{bmatrix}$](img1390.png) を証明せよ.
を証明せよ.
![$ \begin{bmatrix}
0\! & \!c\! & \!b \\ [-0.5ex] c\! & \!0\! & \!a \\ [-0.5ex] b\...
...] ab\! & \!c^2+a^2\! & \!bc \\ [-0.5ex] ca\! & \!bc\! & \!a^2+b^2
\end{bmatrix}$](img1390.png) を証明せよ.
を証明せよ.
問 2.92 (行列の演算)
![$ A \!=\!
\begin{bmatrix}
a_1\! & \!a_2\! & \!a_3 \\ [-0.5ex] 0\! & \!a_4\! & \!a_5 \\ [-0.5ex] 0\! & \!0\! & \!a_6
\end{bmatrix}$](img1391.png) について
について
![$ A {A}^{T}=
\begin{bmatrix}
14\! & \!1\! & \!6 \\ [-0.5ex] 1\! & \!5\! & \!2 \\ [-0.5ex] 6\! & \!2\! & \!4
\end{bmatrix}$](img1392.png) となる
となる  を求めよ.
を求めよ.
![$ A \!=\!
\begin{bmatrix}
a_1\! & \!a_2\! & \!a_3 \\ [-0.5ex] 0\! & \!a_4\! & \!a_5 \\ [-0.5ex] 0\! & \!0\! & \!a_6
\end{bmatrix}$](img1391.png) について
について
![$ A {A}^{T}=
\begin{bmatrix}
14\! & \!1\! & \!6 \\ [-0.5ex] 1\! & \!5\! & \!2 \\ [-0.5ex] 6\! & \!2\! & \!4
\end{bmatrix}$](img1392.png) となる
となる
問 2.93 (乗算の可換性)
![$ X=
\begin{bmatrix}
0\! & \!1 \\ [-0.5ex] -1\! & \!0
\end{bmatrix}$](img1393.png) とおく.
とおく.
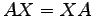 ,
, 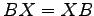 をみたすならば,
をみたすならば, 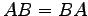 であることを示せ.
であることを示せ.
![$ X=
\begin{bmatrix}
0\! & \!1 \\ [-0.5ex] -1\! & \!0
\end{bmatrix}$](img1393.png) とおく.
とおく.
問 2.94 (乗算の可換性)
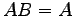 ,
, 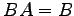 をみたすとき,
をみたすとき,
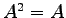 ,
, 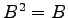 となることを示せ.
となることを示せ.
問 2.95 (乗算の可換性)
次の行列と可換な正方行列をすべて求めよ.
(1)
![$ \begin{bmatrix}
0\! & \!1 \\ [-0.5ex]
-1\! & \!0
\end{bmatrix}$](img1400.png) (2)
(2)
![$ \begin{bmatrix}
1\! & \!1\! & \!0 \\ [-0.5ex]
0\! & \!1\! & \!1 \\ [-0.5ex]
0\! & \!0\! & \!1
\end{bmatrix}$](img1401.png)
問 2.96 (行列の分割)
次の条件式をみたす行列  を求めよ.また,その転置行列
を求めよ.また,その転置行列 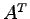 を求めよ.
ただし,
を求めよ.
ただし, 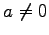 ,
, 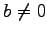 ,
, 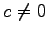 とする.
とする.
(1)![$ \begin{bmatrix}
2a\! & \!3a+2\! & \!-b\! & \!3c \\ [-0.5ex]
-a\! & \!2a-1\! & ...
...]
0\! & \!0\! & \!b\! & \!0 \\ [-0.5ex]
0\! & \!0\! & \!0\! & \!c
\end{bmatrix}$](img1405.png) (2)
(2)
![$ \begin{bmatrix}
-a\! & \!b\! & \!2b+1\! & \!c \\ [-0.5ex]
a\! & \!3b\! & \!b+3...
...
0\! & \!0\! & \!b\! & \!0 \\ [-0.5ex]
0\! & \!0\! & \!0\! & \!c
\end{bmatrix}$](img1406.png)
(1)
![$ \begin{bmatrix}
2a\! & \!3a+2\! & \!-b\! & \!3c \\ [-0.5ex]
-a\! & \!2a-1\! & ...
...]
0\! & \!0\! & \!b\! & \!0 \\ [-0.5ex]
0\! & \!0\! & \!0\! & \!c
\end{bmatrix}$](img1405.png) (2)
(2)
![$ \begin{bmatrix}
-a\! & \!b\! & \!2b+1\! & \!c \\ [-0.5ex]
a\! & \!3b\! & \!b+3...
...
0\! & \!0\! & \!b\! & \!0 \\ [-0.5ex]
0\! & \!0\! & \!0\! & \!c
\end{bmatrix}$](img1406.png)
平成20年2月2日