1.3 ベクトルの演算
定義 1.13 (ベクトルの和)
ベクトル 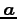 ,
, 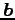 ,
,
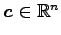 に対して,
ベクトルの和(vector sum)を
に対して,
ベクトルの和(vector sum)を
と定義する.
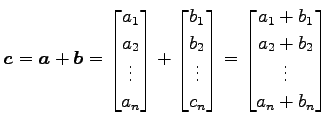 |
(8) |
と定義する.
定義 1.14 (ベクトルのスカラー倍)
ベクトル 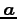 ,
,
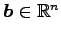 と
スカラー
と
スカラー
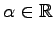 に対して,
ベクトルのスカラー倍(scalar multiple)を
に対して,
ベクトルのスカラー倍(scalar multiple)を
と定義する.
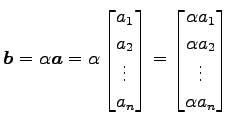 |
(9) |
と定義する.
注意 1.15 (ベクトルの和)
ベクトル 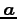 ,
, 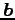 とそれらの和
とそれらの和
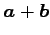 を
考える.
このとき,
点
を
考える.
このとき,
点 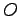 ,
,
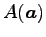 ,
,
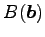 ,
,
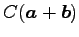 は
平行四辺形となる.
は
平行四辺形となる.
注意 1.16 (ベクトルのスカラー倍)
ベクトル 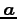 とそのスカラー倍
とそのスカラー倍
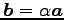 を
考える.
点
を
考える.
点
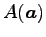 ,
,
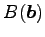 とする.
このとき点
とする.
このとき点  は直線
は直線 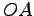 上にある.
線分
上にある.
線分
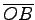 の長さは
線分
の長さは
線分
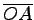 の長さの
の長さの 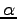 倍である.
倍である.
例 1.17 (ベクトルの和の具体例)
のとき,これらの和は
である.
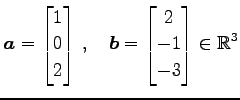 |
(10) |
のとき,これらの和は
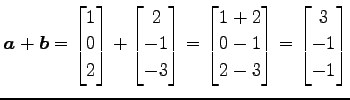 |
(11) |
である.
例 1.18 (ベクトルのスカラー倍の具体例)
のとき,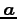 の
の 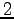 倍は
倍は
である.
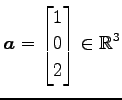 |
(12) |
のとき,
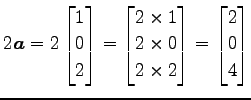 |
(13) |
である.
平成20年2月2日