2.16 行列の分割
![]() 型行列
型行列
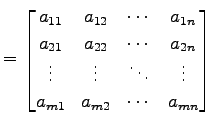 |
(328) |
の
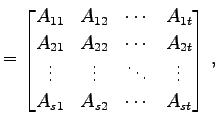 |
(329) | |
| (330) | ||
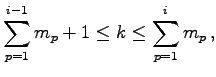 |
(331) | |
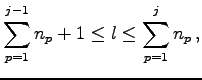 |
(332) | |
| (333) | ||
| (334) | ||
| (335) | ||
| (336) |
と表される. このような表現を
例 2.67 (行列の分割の具体例)
![$\displaystyle = \left[ \begin{array}{c c \vert c} 2 & 3 & 0 \\ 1 & -2 & 0 \\ \h...
...{array}\right]= \begin{bmatrix}A_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix}$](img1218.png) |
(337) |
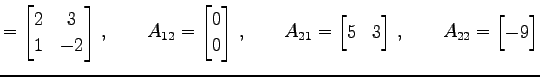 |
(338) |
平成20年2月2日
2.16 行列の分割
型行列
(328)
の個の列を
個の領域に分割し,
個の列を
個の領域に分割する. 縦横で分割された部分領域はそれぞれまた行列となっている. この部分行列をブロック行列(block matrix)と呼び,
と表す.
を用いて行列
を書き直すと
(329) (330) (331) (332) (333) (334) (335) (336)
と表される. このような表現をの分割(partition)という.
を 分割の型(partition type)という.
例 2.67 (行列の分割の具体例)
(337)
(338)
平成20年2月2日