2.15 行列の演算に関する注意
注意 2.55 (積の可換性)
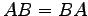 は常に成立するとは限らない.
は常に成立するとは限らない.
定義 2.56 (積の可換性)
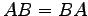 が成立するとき,
が成立するとき,
 と
と  は可換(commutative)であるという.
可換でない場合は非可換(non-commutative)であるという.
は可換(commutative)であるという.
可換でない場合は非可換(non-commutative)であるという.
問 2.57 (積の可換性)
可換となりうる行列は正方行列のみである.
これを示せ.
例 2.58 (非可換な場合の具体例)
行列  ,
,  が
が
で与えられたとする.このとき
となる. よって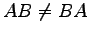 となり,
となり,
 と
と  とは非可換である.
とは非可換である.
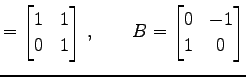 |
(319) |
で与えられたとする.このとき
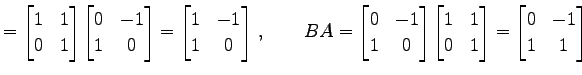 |
(320) |
となる. よって
例 2.59 (可換な場合の具体例)
行列  ,
,  が
が
で与えられたとする.このとき
となる. よって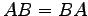 となり,
となり,
 と
と  とは可換である.
とは可換である.
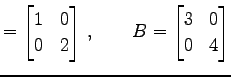 |
(321) |
で与えられたとする.このとき
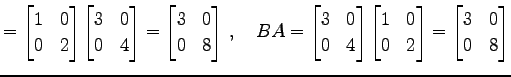 |
(322) |
となる. よって
問 2.60 (対角行列の可換性)
対角行列どうしの積は可換である.これを示せ.
(証明)
対角行列は
![]() ,
,
![]() と表わされる.
これを用いて示す.
と表わされる.
これを用いて示す.
注意 2.61 (行列の方程式)
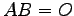 のとき
のとき 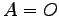 または
または 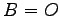 が成立するとは限らない.
数の場合は
が成立するとは限らない.
数の場合は 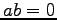 のとき
のとき 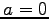 または
または 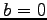 である.
である.
例 2.62 (行列の方程式の具体例)
行列  ,
,  を
を
とする.このとき
となる.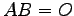 ではあるが
ではあるが 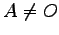 ,
, 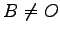 である.
である.
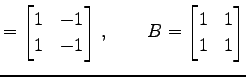 |
(323) |
とする.このとき
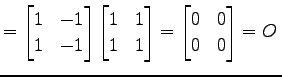 |
(324) |
となる.
定義 2.63 (行列の巾乗)
 が正方行列のとき,
が正方行列のとき, を
を 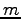 回掛け合わせた行列を
回掛け合わせた行列を
と表記し,これを の巾乗と呼ぶ.
の巾乗と呼ぶ.
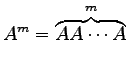 |
(325) |
と表記し,これを
定義 2.64 (巾零行列)
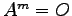 (
(
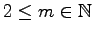 )
を満たす行列
)
を満たす行列  を巾零行列と呼ぶ.
を巾零行列と呼ぶ.
例 2.65 (巾零行列の具体例)
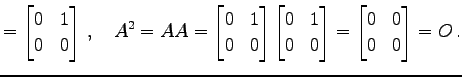 |
(326) | |
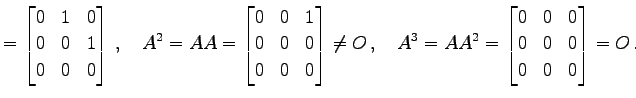 |
(327) |
問 2.66
教科書(p.10)問題 1.2.
平成20年2月2日