2.13 行列の積
定義 2.49 (行列の積)
行列  と行列
と行列  の積を
の積を 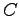 とする.
このとき
とする.
このとき
と表記する. 行列の積は型が
のとき定義される. 各成分は
と定義される.
| (293) |
と表記する. 行列の積は型が
| (294) |
のとき定義される. 各成分は
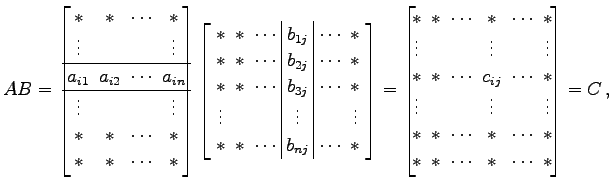 |
(295) | |
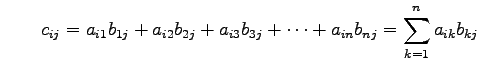 |
(296) |
と定義される.
例 2.50 (行列の積の計算例)
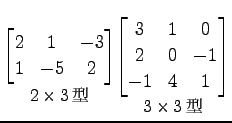 |
(297) | |
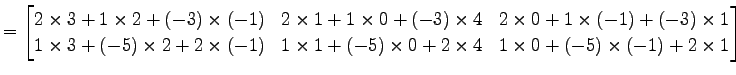 |
(298) | |
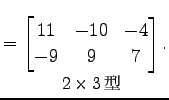 |
(299) |
例 2.51 (行列の積の計算例)
とおく.
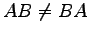 であることに注意.
であることに注意.
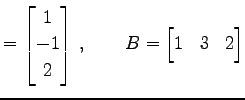 |
(300) |
とおく.
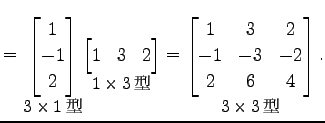 |
(301) | |
 |
(302) |
例 2.52 (行列の積の具体例)
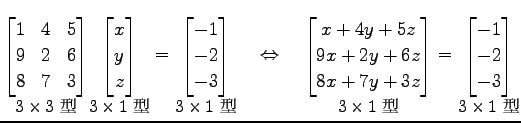 |
(303) | |
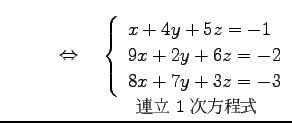 |
(304) |
平成20年2月2日