2.12 行列のスカラー倍
定義 2.46 (行列のスカラー倍)
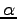 をスカラー(数)とする.
行列
をスカラー(数)とする.
行列  のスカラー倍を
のスカラー倍を
と表記する. 行列のスカラー倍は型が
のとき定義される. 各成分は
と定義される.
| (288) |
と表記する. 行列のスカラー倍は型が
| (289) |
のとき定義される. 各成分は
| (290) |
と定義される.
例 2.47 (スカラー倍の計算例)
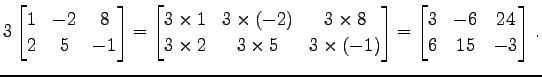 |
(291) |
例 2.48 (スカラー倍の計算例)
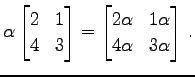 |
(292) |
平成20年2月2日