2.6 行列のいろいろ 〜 対称行列，交代行列

定義 2.21 (対称行列) 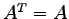  ${A}^{T}=A$ を満たす行列を 対称行列（symmetric matrix）と呼ぶ．

例 2.22 (対称行列の具体例)  

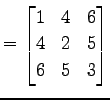$$A = \begin{bmatrix}1 & 4 & 6 \\ 4 & 2 & 5 \\ 6 & 5 & 3 \end{bmatrix}$$ (272)

問 2.23 (対称行列の一般的な表現)   対称行列は正方行列で一般に

$$A = \begin{bmatrix}a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ a_... ...& \ddots & \vdots \\ a_{1n} & a_{2n} & a_{3n} & \cdots & a_{nn} \end{bmatrix}\,$$ (273)

と表わされる． これを示せ．

定義 2.24 (歪対称行列) 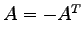  $A=-{A}^{T}$ を満たす行列を 歪対称行列（skew symmetric matrix） または， 交代行列（alternative matrix） と呼ぶ．

例 2.25 (歪対称行列の具体例)  

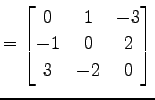$$A = \begin{bmatrix}0 & 1 & -3 \\ -1 & 0 & 2 \\ 3 & -2 & 0 \end{bmatrix}$$ (274)

問 2.26 (対称行列の一般的な表現)   歪対称行列は正方行列で一般に

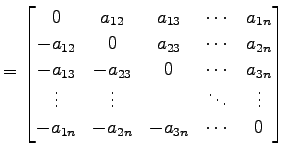$$A = \begin{bmatrix}0 & a_{12} & a_{13} & \cdots & a_{1n} \\ -a_{12}... ...s & & \ddots & \vdots \\ -a_{1n} &-a_{2n} &-a_{3n} & \cdots & 0 \end{bmatrix}\,$$ (275)

と表わされる． これを示せ．

問 2.27   教科書（p.5）問題 1.1.

注意 2.28 (歪対称行列)   交代行列の対角成分はすべて 0 である．

平成20年2月2日