2.1 行列
定義 2.1
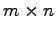 個の数
個の数
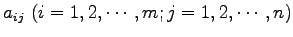 を
を
と並べたものを行列(matrix)とよぶ. このとき行列 は
は
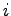 行
行 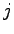 列番目の数を
列番目の数を
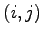 成分(component)
または要素(element)
と呼ぶ.
成分(component)
または要素(element)
と呼ぶ.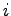 番目の行
番目の行
を第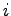 行(the
行(the 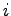 -th row)という.
-th row)という.
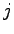 番目の列
番目の列
を第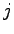 列(the
列(the 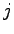 -th column)という.
行列
-th column)という.
行列  を省略して書くときは
を省略して書くときは
のようにする.
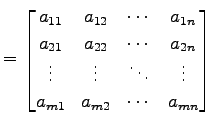 |
(250) |
と並べたものを行列(matrix)とよぶ. このとき行列
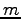 行
行 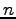 列の行列
列の行列
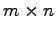 型の行列
型の行列
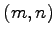 行列
行列
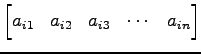 |
(251) |
を第
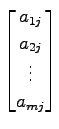 |
(252) |
を第
| (253) |
のようにする.
平成20年2月2日