1.1 ベクトル
ベクトルの定義は主に三つある.
定義 1.1 (ベクトルその1)
位置の違いを無視して,
向きと大きさをもつ量
(矢印,有向線分(oriented segment))を
ベクトル(vector)という.
これに対して方向をもたない普通の量をスカラー(scalar)
という.
注意 1.2 (ベクトルの平行移動は同じもの)
始点(initial point)  から
終点(terminal point)
から
終点(terminal point)  への有向線分を
表すベクトルを
への有向線分を
表すベクトルを
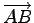 と表記する.
ベクトル
と表記する.
ベクトル
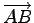 と
ベクトル
と
ベクトル
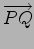 とを原点に平行移動したとき
これらのベクトルが等しければ,
とを原点に平行移動したとき
これらのベクトルが等しければ,
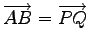 である.
すなわち,
ベクトルは平行移動しても同じ量であるとみなす.
たくさんある同じベクトルのうち代表して始点が原点にあるものを選ぶ.
である.
すなわち,
ベクトルは平行移動しても同じ量であるとみなす.
たくさんある同じベクトルのうち代表して始点が原点にあるものを選ぶ.
定義 1.3 (ベクトルその2)
列ベクトル(column vector)
と行ベクトル(row vector)
を総称してベクトル(vector)という. 括弧の中の値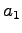 ,
,  ,
, 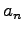 をベクトルの
成分(component)または要素(element)という.
をベクトルの
成分(component)または要素(element)という.
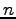 次の列ベクトル全体の集合を
次の列ベクトル全体の集合を
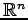 で表す.
で表す.
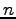 次の行ベクトル全体の集合を
次の行ベクトル全体の集合を
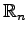 で表す.
で表す.
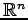 ,
,
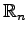 を
を
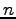 次元実ベクトル空間(
次元実ベクトル空間(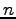 -dimensional real vector space)
という.
また,要素が複素数の場合は
-dimensional real vector space)
という.
また,要素が複素数の場合は
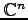 ,
,
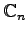 と表し,
と表し,
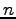 次元複素ベクトル空間(
次元複素ベクトル空間(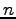 -dimensional complex vector space)
という.
-dimensional complex vector space)
という.
| (1) |
と行ベクトル(row vector)
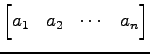 |
(2) |
を総称してベクトル(vector)という. 括弧の中の値
注意 1.4 (括弧)
行ベクトル,列ベクトルの括弧は,
丸い括弧でも角張った括弧でもどちらを使ってもかまわない:
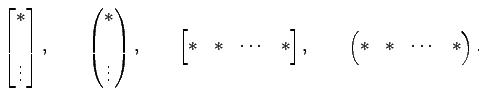 |
(3) |
注意 1.5 (列ベクトル,行ベクトル)
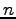 次の列ベクトルは
次の列ベクトルは 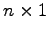 行列である.
行列である.
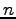 次の行ベクトルは
次の行ベクトルは 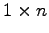 行列である.
行列である.
注意 1.6 (列ベクトル,行ベクトル)
列ベクトル,行ベクトルともに,以下の議論全てに渡って同じ性質をもつ.
そのため,基本的にはどちらで議論してもかまわない.
しかし,本講義ではベクトルは全て列ベクトルとして取り扱う.
なぜなら,線形変換においてベクトルは列ベクトルとして取り扱う方が
議論がしやすいためである.
さらにいうと,線形変換における性質で,
列ベクトルと行ベクトルを使い分けるときもある.
位置ベクトル,方向ベクトルは列ベクトルとして取扱い,
反変ベクトル(contravariant vector)という.
法線ベクトルは行ベクトルとして取り扱い,
共変ベクトル(covariant vector)という.
定義 1.7 (ベクトルその3)
ベクトル空間(vector space) 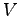 の元
の元 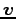 を
ベトクル(vector)という.
を
ベトクル(vector)という.
平成20年2月2日