1.23 単位ベクトル
定義 1.118 (単位ベクトル)
ノルムが 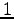 のベクトルを
単位ベクトル(unit vectar) という.
のベクトルを
単位ベクトル(unit vectar) という.
例 1.119 (単位ベクトルの具体例)
は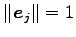 であり全て単位ベクトルである.
であり全て単位ベクトルである.
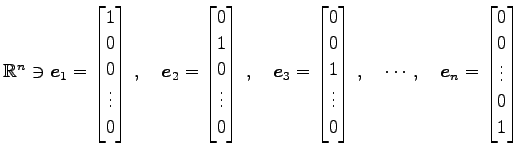 |
(128) |
は
定義 1.120 (正規化)
あるベクトルを向きが同じで長さが 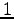 のベクトルに
変換することを正規化(normalization)という.
のベクトルに
変換することを正規化(normalization)という.
例 1.121 (正規化の具体例)
ベクトル
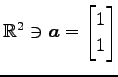 を正規化し
を正規化し
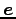 とする.
すなわち
とする.
すなわち
と得られる.
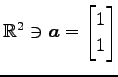 を正規化し
を正規化し
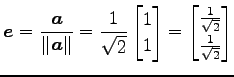 |
(129) |
と得られる.
定義 1.122 (単位方向ベクトル,単位法線ベクトル)
長さが 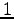 の方向ベクトルを
単位方向ベクトル(unit tangent vector)という.
長さが
の方向ベクトルを
単位方向ベクトル(unit tangent vector)という.
長さが 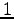 の法線ベクトルを
単位法線ベクトル(unit normal vector)という.
の法線ベクトルを
単位法線ベクトル(unit normal vector)という.
例 1.123 (単位ベクトル)
方程式
の単位方向ベクトルは
であり, 単位法線ベクトルは
である.
| (130) |
の単位方向ベクトルは
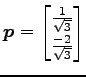 |
(131) |
であり, 単位法線ベクトルは
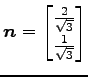 |
(132) |
である.
平成20年2月2日