1.20 外積をベクトルで計算
例 1.96 (外積の計算例)
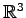 の軸
の軸 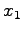 ,
, 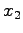 ,
, 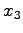 と
同じ向きの単位ベクトル
と
同じ向きの単位ベクトル
を考える.このとき
が成り立つ.
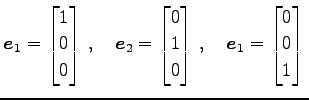 |
(110) |
を考える.このとき
| (111) | ||
| (112) | ||
| (113) |
が成り立つ.
例 1.97 (外積の計算例)
を考える.このとき外積は
となる.
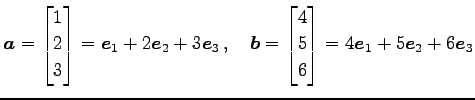 |
(114) |
を考える.このとき外積は
| (115) | ||
| (116) | ||
| (117) | ||
| (118) | ||
| (119) | ||
| (120) | ||
| (121) | ||
| (122) | ||
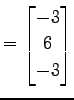 |
(123) |
となる.
平成20年2月2日