1.18 外積の性質
定理 1.88 (外積の性質)
- (i)
-
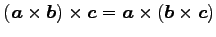 (結合則)
(結合則)
- (ii)
-
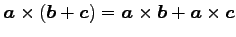 ,
,
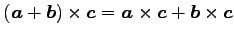 (分配則)
(分配則)
- (iii)
-
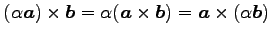 (スカラー倍の結合則)
(スカラー倍の結合則)
- (iv)
-
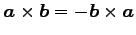 (交換則)
(交換則)
- (v)
-
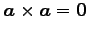
- (vi)
-
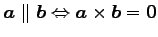
問 1.89 (外積の性質)
これを示せ.
(証明)
(iv) 積の順を入れ換えると向きが反対向きになるため.
(v) 自分自身との角度は ![]() であるから長さは 0 となり,
外積は
であるから長さは 0 となり,
外積は ![]() である.
(vi)
である.
(vi) ![]() と
と ![]() が並行なとき
が並行なとき
![]() であるから長さは 0 となり,
外積は
であるから長さは 0 となり,
外積は ![]() である.
である.
注意 1.90 (内積の性質)
外積の性質と内積の性質の違いに注意する:
- (i)
-
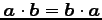 .
.
- (ii)
-
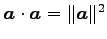 .
.
- (iii)
-
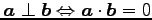 .
.
問 1.91 (外積の性質)
次の関係式を示せ.
(1)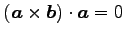 (2)
(2)
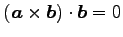 (3)
(3)
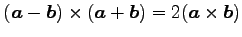
(4)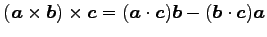 ,
,
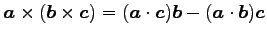 .
これをベクトル
.
これをベクトル 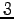 重積 (vector triple product)または
ラグランジュの公式 (Lagrange's formula)という.
重積 (vector triple product)または
ラグランジュの公式 (Lagrange's formula)という.
(5)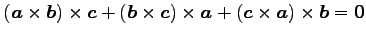 .
これをヤコビの公式 (Jacobi's formula)という.
.
これをヤコビの公式 (Jacobi's formula)という.
(6)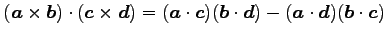
(7)![$ \displaystyle{
\vec{a}\cdot(\vec{b}\times(\vec{c}\times\vec{d}))=
(\vec{a}\tim...
...cdot\vec{c} \\ [-.3ex]
\vec{a}\cdot\vec{d} &
\vec{b}\cdot\vec{d}
\end{vmatrix}}$](img465.png)
(1)
(4)
(5)
(6)
(7)
![$ \displaystyle{
\vec{a}\cdot(\vec{b}\times(\vec{c}\times\vec{d}))=
(\vec{a}\tim...
...cdot\vec{c} \\ [-.3ex]
\vec{a}\cdot\vec{d} &
\vec{b}\cdot\vec{d}
\end{vmatrix}}$](img465.png)
平成20年2月2日