4.21 演習問題 〜 余因子行列,クラメルの公式
問 4.115 (余因子行列)
次の行列の逆行列を余因子行列を用いて求めよ.
(1)![$ \begin{bmatrix}
3\! & \!-1 \\ [-0.5ex] 1\! & \!2
\end{bmatrix}$](img2388.png) (2)
(2)
![$ \begin{bmatrix}
2\! & \!1 \\ [-0.5ex] -5\! & \!-4
\end{bmatrix}$](img2389.png) (3)
(3)
![$ \begin{bmatrix}
\cos\theta\! & \!-\sin\theta \\ [-0.5ex] \sin\theta\! & \!\cos\theta
\end{bmatrix}$](img2390.png) (4)
(4)
![$ \frac{1}{2}
\begin{bmatrix}
1\! & \!-\sqrt{3} \\ [-0.5ex] \sqrt{3}\! & \!1
\end{bmatrix}$](img2391.png) (5)
(5)
![$ \begin{bmatrix}
1\! & \!2\! & \!3 \\ [-0.5ex] 1\! & \!1\! & \!-1 \\ [-0.5ex] 4\! &
1\! & \!5
\end{bmatrix}$](img2392.png)
(6)![$ \begin{bmatrix}
1\! & \!-2\! & \!2 \\ [-0.5ex] 4\! & \!1\! & \!-1 \\ [-0.5ex] 2\! &
-1\! & \!3
\end{bmatrix}$](img2393.png) (7)
(7)
![$ \begin{bmatrix}
2\! & \!4\! & \!1 \\ [-0.5ex] 1\! & \!-2\! & \!1 \\ [-0.5ex] 0\! &
5\! & \!-1
\end{bmatrix}$](img2394.png) (8)
(8)
![$ \begin{bmatrix}
2\! & \!-1\! & \!-2 \\ [-0.5ex] -1\! & \!0\! & \!3 \\ [-0.5ex] 3\! &
-2\! & \!5
\end{bmatrix}$](img2395.png) (9)
(9)
![$ \begin{bmatrix}
a\! & \!0\! & \!0 \\ [-0.5ex] d\! & \!b\! & \!0 \\ [-0.5ex] e\! &
f\! & \!c
\end{bmatrix}$](img2396.png) (10)
(10)
![$ \begin{bmatrix}
2\! & \!1\! & \!0 \\ [-0.5ex] 1\! & \!-1\! & \!2 \\ [-0.5ex] -1\! &
0\! & \!-1
\end{bmatrix}$](img2397.png)
(11)![$ \begin{bmatrix}
x-2\! & \!1\! & \!1 \\ [-0.5ex] 0\! & \!2x-1\! & \!x-1 \\ [-0.5ex] -2\! &
1\! & \!1
\end{bmatrix}$](img2398.png) (12)
(12)
![$ \begin{bmatrix}
1\! & \!0\! & \!1 \\ [-0.5ex] 2\! & \!2\! & \!3 \\ [-0.5ex] 1\! &
-1\! & \!1
\end{bmatrix}$](img2399.png) (13)
(13)
![$ \begin{bmatrix}
2\! & \!3\! & \!2 \\ [-0.5ex] 3\! & \!1\! & \!-2 \\ [-0.5ex] -1\! &
0\! & \!1
\end{bmatrix}$](img2400.png) (14)
(14)
![$ \begin{bmatrix}
3\! & \!1\! & \!0 \\ [-0.5ex] 2\! & \!1\! & \!1 \\ [-0.5ex] 1\! &
0\! & \!1
\end{bmatrix}$](img2401.png)
(15)![$ \begin{bmatrix}
2\! & \!-1\! & \!1 \\ [-0.5ex] 1\! & \!2\! & \!-2 \\ [-0.5ex] 3\! &
1\! & \!0
\end{bmatrix}$](img2402.png) (16)
(16)
![$ \begin{bmatrix}
1\! & \!-2\! & \!0 \\ [-0.5ex] 2\! & \!-1\! & \!1 \\ [-0.5ex] 0\! &
3\! & \!1
\end{bmatrix}$](img2403.png) (17)
(17)
![$ \begin{bmatrix}
1\! & \!0\! & \!2 \\ [-0.5ex] 2\! & \!-3\! & \!4 \\ [-0.5ex] 0\! &
2\! & \!1
\end{bmatrix}$](img2404.png) (18)
(18)
![$ \begin{bmatrix}
1\! & \!2\! & \!-3 \\ [-0.5ex] 2\! & \!-3\! & \!1 \\ [-0.5ex] 8\! &
1\! & \!-5
\end{bmatrix}$](img2405.png)
(1)
![$ \begin{bmatrix}
3\! & \!-1 \\ [-0.5ex] 1\! & \!2
\end{bmatrix}$](img2388.png) (2)
(2)
![$ \begin{bmatrix}
2\! & \!1 \\ [-0.5ex] -5\! & \!-4
\end{bmatrix}$](img2389.png) (3)
(3)
![$ \begin{bmatrix}
\cos\theta\! & \!-\sin\theta \\ [-0.5ex] \sin\theta\! & \!\cos\theta
\end{bmatrix}$](img2390.png) (4)
(4)
![$ \frac{1}{2}
\begin{bmatrix}
1\! & \!-\sqrt{3} \\ [-0.5ex] \sqrt{3}\! & \!1
\end{bmatrix}$](img2391.png) (5)
(5)
![$ \begin{bmatrix}
1\! & \!2\! & \!3 \\ [-0.5ex] 1\! & \!1\! & \!-1 \\ [-0.5ex] 4\! &
1\! & \!5
\end{bmatrix}$](img2392.png)
(6)
![$ \begin{bmatrix}
1\! & \!-2\! & \!2 \\ [-0.5ex] 4\! & \!1\! & \!-1 \\ [-0.5ex] 2\! &
-1\! & \!3
\end{bmatrix}$](img2393.png) (7)
(7)
![$ \begin{bmatrix}
2\! & \!4\! & \!1 \\ [-0.5ex] 1\! & \!-2\! & \!1 \\ [-0.5ex] 0\! &
5\! & \!-1
\end{bmatrix}$](img2394.png) (8)
(8)
![$ \begin{bmatrix}
2\! & \!-1\! & \!-2 \\ [-0.5ex] -1\! & \!0\! & \!3 \\ [-0.5ex] 3\! &
-2\! & \!5
\end{bmatrix}$](img2395.png) (9)
(9)
![$ \begin{bmatrix}
a\! & \!0\! & \!0 \\ [-0.5ex] d\! & \!b\! & \!0 \\ [-0.5ex] e\! &
f\! & \!c
\end{bmatrix}$](img2396.png) (10)
(10)
![$ \begin{bmatrix}
2\! & \!1\! & \!0 \\ [-0.5ex] 1\! & \!-1\! & \!2 \\ [-0.5ex] -1\! &
0\! & \!-1
\end{bmatrix}$](img2397.png)
(11)
![$ \begin{bmatrix}
x-2\! & \!1\! & \!1 \\ [-0.5ex] 0\! & \!2x-1\! & \!x-1 \\ [-0.5ex] -2\! &
1\! & \!1
\end{bmatrix}$](img2398.png) (12)
(12)
![$ \begin{bmatrix}
1\! & \!0\! & \!1 \\ [-0.5ex] 2\! & \!2\! & \!3 \\ [-0.5ex] 1\! &
-1\! & \!1
\end{bmatrix}$](img2399.png) (13)
(13)
![$ \begin{bmatrix}
2\! & \!3\! & \!2 \\ [-0.5ex] 3\! & \!1\! & \!-2 \\ [-0.5ex] -1\! &
0\! & \!1
\end{bmatrix}$](img2400.png) (14)
(14)
![$ \begin{bmatrix}
3\! & \!1\! & \!0 \\ [-0.5ex] 2\! & \!1\! & \!1 \\ [-0.5ex] 1\! &
0\! & \!1
\end{bmatrix}$](img2401.png)
(15)
![$ \begin{bmatrix}
2\! & \!-1\! & \!1 \\ [-0.5ex] 1\! & \!2\! & \!-2 \\ [-0.5ex] 3\! &
1\! & \!0
\end{bmatrix}$](img2402.png) (16)
(16)
![$ \begin{bmatrix}
1\! & \!-2\! & \!0 \\ [-0.5ex] 2\! & \!-1\! & \!1 \\ [-0.5ex] 0\! &
3\! & \!1
\end{bmatrix}$](img2403.png) (17)
(17)
![$ \begin{bmatrix}
1\! & \!0\! & \!2 \\ [-0.5ex] 2\! & \!-3\! & \!4 \\ [-0.5ex] 0\! &
2\! & \!1
\end{bmatrix}$](img2404.png) (18)
(18)
![$ \begin{bmatrix}
1\! & \!2\! & \!-3 \\ [-0.5ex] 2\! & \!-3\! & \!1 \\ [-0.5ex] 8\! &
1\! & \!-5
\end{bmatrix}$](img2405.png)
問 4.116 (余因子行列)
 は
は 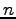 次の正方行列とする.このとき余因子行列
次の正方行列とする.このとき余因子行列 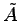 が
が
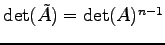 であることを示せ.
であることを示せ.
問 4.117 (余因子行列)
 が対称行列ならば余因子行列
が対称行列ならば余因子行列 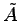 も対称行列であることを示せ.
また
も対称行列であることを示せ.
また  がさらに正則ならば
がさらに正則ならば 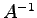 も対称行列であることを示せ.
も対称行列であることを示せ.
問 4.118 (余因子行列)
 が交代行列のとき余因子行列
が交代行列のとき余因子行列 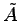 は交代行列となるか答えよ.
は交代行列となるか答えよ.
問 4.119 (クラメルの公式)
次の連立方程式をクラメルの公式を用いて解け.
(1)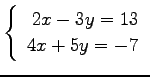 (2)
(2)
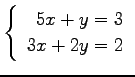 (3)
(3)
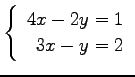 (4)
(4)
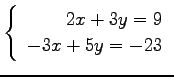
(5)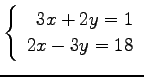 (6)
(6)
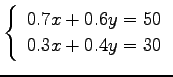 (7)
(7)
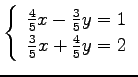 (8)
(8)
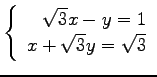
(9)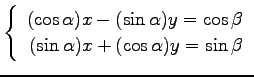 (10)
(10)
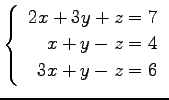 (11)
(11)
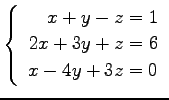
(12)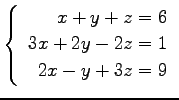 (13)
(13)
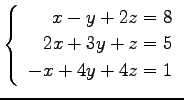 (14)
(14)
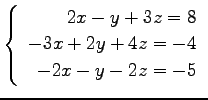
(15)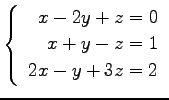 (16)
(16)
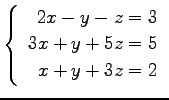 (17)
(17)
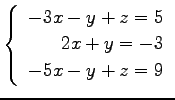
(18)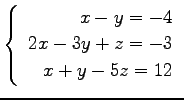 (19)
(19)
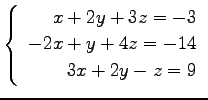 (20)
(20)
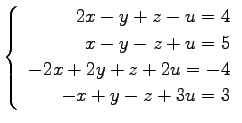
(21)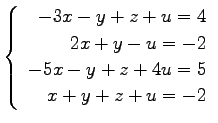 (22)
(22)
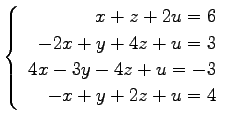
(1)
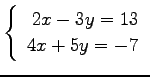 (2)
(2)
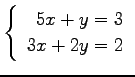 (3)
(3)
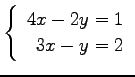 (4)
(4)
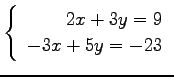
(5)
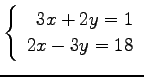 (6)
(6)
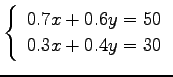 (7)
(7)
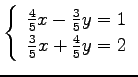 (8)
(8)
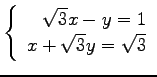
(9)
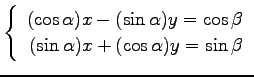 (10)
(10)
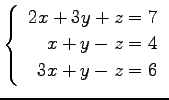 (11)
(11)
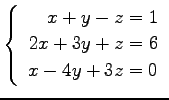
(12)
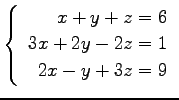 (13)
(13)
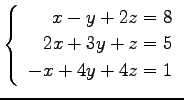 (14)
(14)
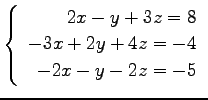
(15)
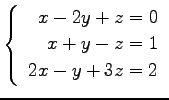 (16)
(16)
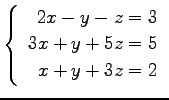 (17)
(17)
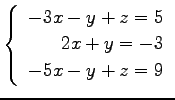
(18)
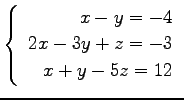 (19)
(19)
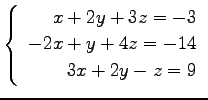 (20)
(20)
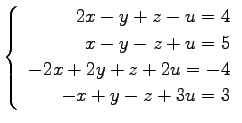
(21)
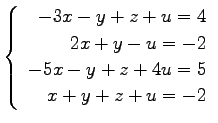 (22)
(22)
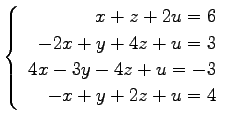
問 4.120 (クラメルの公式)
次の方程式が一意な解をもつための条件とそのときの解を定めよ.
(1)![$ \begin{bmatrix}
a\! & \!0\! & \!b \\ [-0.5ex] b\! & \!a\! & \!0 \\ [-0.5ex] b\...
...x] z
\end{bmatrix}=
\begin{bmatrix}
b \\ [-0.5ex] 1 \\ [-0.5ex] a
\end{bmatrix}$](img2428.png) (2)
(2)
![$ \begin{bmatrix}
1\! & \!1\! & \!1 \\ [-0.5ex] a\! & \!b\! & \!c \\ [-0.5ex] a^...
...x] z
\end{bmatrix}=
\begin{bmatrix}
0 \\ [-0.5ex] 1 \\ [-0.5ex] 0
\end{bmatrix}$](img2429.png) (3)
(3)
![$ \begin{bmatrix}
0\! & \!a\! & \!1 \\ [-0.5ex] 1\! & \!0\! & \!c \\ [-0.5ex] b\...
...x] z
\end{bmatrix}=
\begin{bmatrix}
a \\ [-0.5ex] b \\ [-0.5ex] c
\end{bmatrix}$](img2430.png)
(4)![$ \begin{bmatrix}
1\! & \!1\! & \!1 \\ [-0.5ex] a\! & \!1\! & \!a \\ [-0.5ex] b\...
...] z
\end{bmatrix}=
\begin{bmatrix}
1 \\ [-0.5ex] 0 \\ [-0.5ex] -1
\end{bmatrix}$](img2431.png)
(1)
![$ \begin{bmatrix}
a\! & \!0\! & \!b \\ [-0.5ex] b\! & \!a\! & \!0 \\ [-0.5ex] b\...
...x] z
\end{bmatrix}=
\begin{bmatrix}
b \\ [-0.5ex] 1 \\ [-0.5ex] a
\end{bmatrix}$](img2428.png) (2)
(2)
![$ \begin{bmatrix}
1\! & \!1\! & \!1 \\ [-0.5ex] a\! & \!b\! & \!c \\ [-0.5ex] a^...
...x] z
\end{bmatrix}=
\begin{bmatrix}
0 \\ [-0.5ex] 1 \\ [-0.5ex] 0
\end{bmatrix}$](img2429.png) (3)
(3)
![$ \begin{bmatrix}
0\! & \!a\! & \!1 \\ [-0.5ex] 1\! & \!0\! & \!c \\ [-0.5ex] b\...
...x] z
\end{bmatrix}=
\begin{bmatrix}
a \\ [-0.5ex] b \\ [-0.5ex] c
\end{bmatrix}$](img2430.png)
(4)
![$ \begin{bmatrix}
1\! & \!1\! & \!1 \\ [-0.5ex] a\! & \!1\! & \!a \\ [-0.5ex] b\...
...] z
\end{bmatrix}=
\begin{bmatrix}
1 \\ [-0.5ex] 0 \\ [-0.5ex] -1
\end{bmatrix}$](img2431.png)
平成20年2月2日