5.2 演習 〜 べき級数
問 5.8 (べき級数)
べき級数
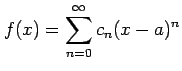 は
(i)
は
(i)
![$ \displaystyle{r= \lim_{n \to\infty}\frac{1}{\sqrt[n]{\vert c_n\vert}}}$](img1709.png) ,
(ii)
,
(ii)
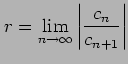 が存在するとき
が存在するとき
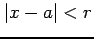 において絶対収束することを示せ.
において絶対収束することを示せ.
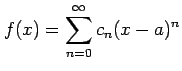 は
(i)
は
(i)
![$ \displaystyle{r= \lim_{n \to\infty}\frac{1}{\sqrt[n]{\vert c_n\vert}}}$](img1709.png) ,
(ii)
,
(ii)
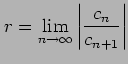 が存在するとき
が存在するとき
問 5.9 (べき級数)
次のべき級数の収束半径を求めよ.
(1)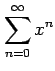 (2)
(2)
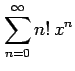 (3)
(3)
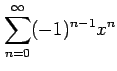 (4)
(4)
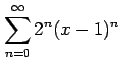 (5)
(5)
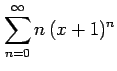
(6)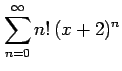 (7)
(7)
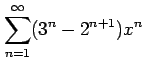 (8)
(8)
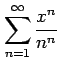 (9)
(9)
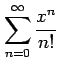 (10)
(10)
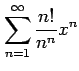
(11)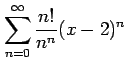 (12)
(12)
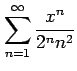 (13)
(13)
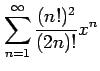 (14)
(14)
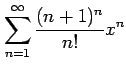 (15)
(15)
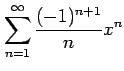
(16)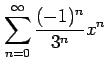 (17)
(17)
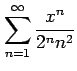 (18)
(18)
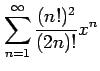 (19)
(19)
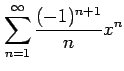
(20)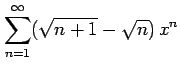 (21)
(21)
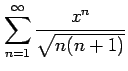 (22)
(22)
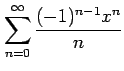 (23)
(23)
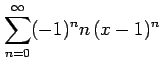
(1)
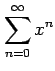 (2)
(2)
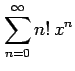 (3)
(3)
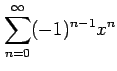 (4)
(4)
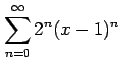 (5)
(5)
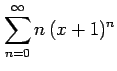
(6)
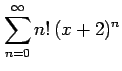 (7)
(7)
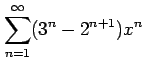 (8)
(8)
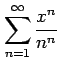 (9)
(9)
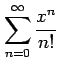 (10)
(10)
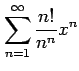
(11)
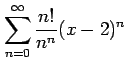 (12)
(12)
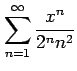 (13)
(13)
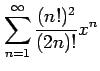 (14)
(14)
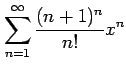 (15)
(15)
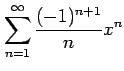
(16)
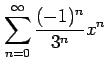 (17)
(17)
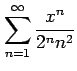 (18)
(18)
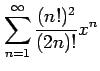 (19)
(19)
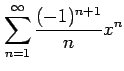
(20)
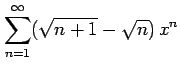 (21)
(21)
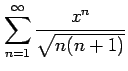 (22)
(22)
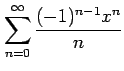 (23)
(23)
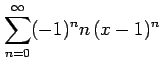
平成19年10月3日