2.42 演習 〜 連続
問 2.155 (連続)
次の関数  がそれぞれ[ ]内に指定された点において連続であるか述べよ.
がそれぞれ[ ]内に指定された点において連続であるか述べよ.
(1)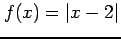
![$ [x=2]$](img766.png) (2)
(2)
![\begin{displaymath}f(x)= \left\{
\begin{array}{ccc}
\displaystyle{\frac{x}{\vert...
...} & (x\neq 0)&\\
&&\quad[x=0]\\
0 & (x=0)&
\end{array}\right.\end{displaymath}](img767.png)
(1)
![\begin{displaymath}f(x)= \left\{
\begin{array}{ccc}
\displaystyle{\frac{x}{\vert...
...} & (x\neq 0)&\\
&&\quad[x=0]\\
0 & (x=0)&
\end{array}\right.\end{displaymath}](img767.png)
問 2.156 (連続)
次の関数が連続となる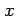 の範囲を定めよ.
の範囲を定めよ.
(1)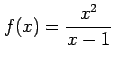 (2)
(2)
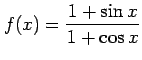 (3)
(3)
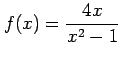 (4)
(4)
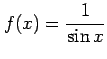
(5)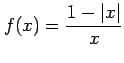 (6)
(6)
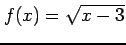
(1)
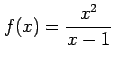 (2)
(2)
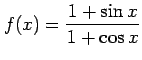 (3)
(3)
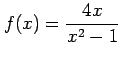 (4)
(4)
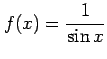
(5)
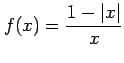 (6)
(6)
問 2.157 (連続)
次の関数  を
を 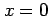 で連続となるように
で連続となるように 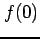 の値を定義せよ.
の値を定義せよ.
(1)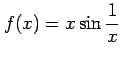
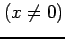 (2)
(2)
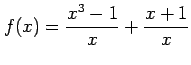
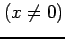
(3)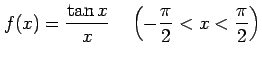
(1)
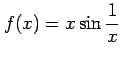
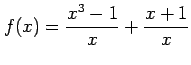
(3)
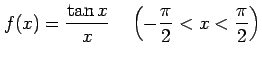
問 2.158 (連続)
次の関数が連続関数となるように不連続点での値を定義せよ.
(1)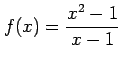 (2)
(2)
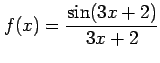
(1)
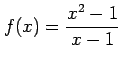 (2)
(2)
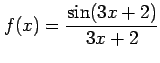
平成19年10月3日