2.9 関数のかたち
定義 2.32 (単調関数)
関数  が
が
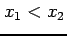 をみたす
任意の点
をみたす
任意の点 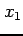 ,
, 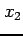 (
(
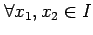 ) に対して
) に対して
-
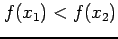 が成り立つとき,
関数
が成り立つとき,
関数  は単調増加(monotonic increasing)であると呼ぶ.
は単調増加(monotonic increasing)であると呼ぶ.
-
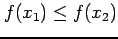 が成り立つとき,
関数
が成り立つとき,
関数  は
広義の単調増加(monotonic increasing in the wider sense)で
あると呼ぶ.
は
広義の単調増加(monotonic increasing in the wider sense)で
あると呼ぶ.
-
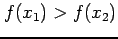 が成り立つとき,
関数
が成り立つとき,
関数  は単調減少(monotonic decreasing)であると呼ぶ.
は単調減少(monotonic decreasing)であると呼ぶ.
-
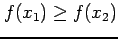 が成り立つとき,
関数
が成り立つとき,
関数  は
広義の単調減少(monotonic decreasing in the wider sense)で
あると呼ぶ.
は
広義の単調減少(monotonic decreasing in the wider sense)で
あると呼ぶ.
例 2.33 (単調関数の具体例)
関数 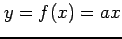 を考える.
を考える.
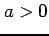 のとき
のとき  は
は
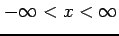 において単調増加である.
また
において単調増加である.
また 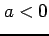 のときは
のときは  は
は
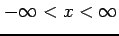 において単調減少となる.
なぜなら
において単調減少となる.
なぜなら
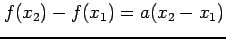 であり,
であり,
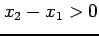 であることより,
であることより,
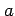 の符号により
の符号により 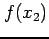 と
と 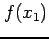 の大小関係が
定まるからである.
の大小関係が
定まるからである.
定義 2.34 (周期関数)
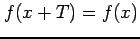 をみたす関数を
周期関数(periodic function)と呼ぶ.
をみたす関数を
周期関数(periodic function)と呼ぶ.
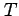 を周期(period)と呼ぶ.
を周期(period)と呼ぶ.
定義 2.35 (奇関数,偶関数)
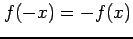 をみたす関数を
奇関数(odd function)と呼ぶ.
をみたす関数を
奇関数(odd function)と呼ぶ.
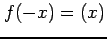 をみたす関数を
偶関数(even function)と呼ぶ.
をみたす関数を
偶関数(even function)と呼ぶ.
問 2.36
奇関数は原点に関して点対称のグラフとなる.
偶関数は 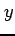 軸に関して線対称なグラフとなる.
これを示せ.
軸に関して線対称なグラフとなる.
これを示せ.
平成19年10月3日