2.8 多価関数
定義 2.29 (一価関数,多価関数)
ある一つの 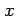 の値に対して
の値に対して 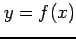 の値が
の値が 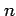 個定まるとき,
個定まるとき,
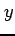 は
は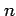 価(
価(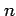 -valued function)
であるという.
すべての
-valued function)
であるという.
すべての 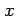 に対して
に対して 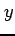 が
が 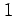 価であるとき
価であるとき 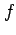 を
を
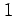 価関数(single valued function) という.
価関数(single valued function) という.
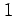 価関数ではないとき多価関数(many valued function)
という.
価関数ではないとき多価関数(many valued function)
という.
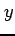 が最大で
が最大で 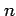 価となるとき
価となるとき 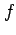 を
を
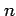 価関数(
価関数(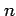 -valued function) という.
-valued function) という.
定義 2.30 (枝,主枝,主値)
多価関数が一価関数となるように値域を限定する.
このとき得られる一価関数それぞれを分枝(branch)と呼ぶ.
この分枝のうち代表する一つを
主分枝(principal branch)と呼ぶ.
主分岐は主値(principal value)ともいう.
例 2.31 (一価関数,多価関数,逆関数,分枝の具体例)
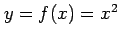 は一価関数である.
この関数の逆関数は
は一価関数である.
この関数の逆関数は
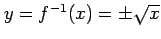 であり 2 価関数となる.
値域を
であり 2 価関数となる.
値域を 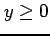 と
と 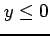 とに限定すると
一価関数が二つ得られる.
すなわち分枝は
とに限定すると
一価関数が二つ得られる.
すなわち分枝は
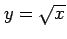 と
と
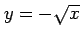 である.
である.
平成19年10月3日