2.5 逆写像
定義 2.16 (逆写像)
写像 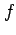 に対して
に対して
をみたす写像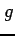 が存在するとき,
写像
が存在するとき,
写像 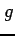 を
を 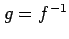 と表記し,
と表記し,
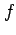 の逆写像(inverse mapping)という.
の逆写像(inverse mapping)という.
をみたす写像
定理 2.17 (逆写像)
写像 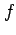 が全単射のとき逆写像
が全単射のとき逆写像 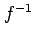 は存在する.
は存在する.
例 2.18 (逆写像)
写像
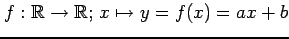 の逆写像は
の逆写像は
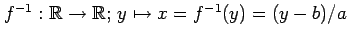 である.
である.
例 2.19 (逆写像)
写像
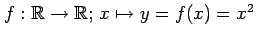 は
全単射ではないので逆写像は存在しない.
ただし,集合
は
全単射ではないので逆写像は存在しない.
ただし,集合
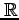 を非負に制限した集合
を非負に制限した集合
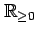 に
おける写像
に
おける写像
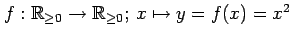 を考えれば,この逆写像は
を考えれば,この逆写像は
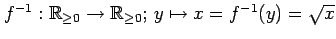 となる.
となる.
平成19年10月3日