5.22 関数の増減と極値
定義 5.57 (増加,減少,極値)
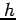 を十分小さい正の数
を十分小さい正の数 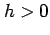 とする.
このとき関数
とする.
このとき関数  に関して次の性質を定義する.
に関して次の性質を定義する.
-
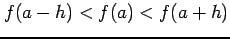 をみたすとき,
関数
をみたすとき,
関数  は点
は点 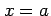 において増加の状態
であるという.
において増加の状態
であるという.
-
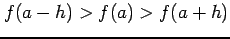 をみたすとき,
関数
をみたすとき,
関数  は点
は点 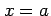 において減少の状態
であるという.
において減少の状態
であるという.
-
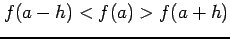 をみたすとき,
関数
をみたすとき,
関数  は点
は点 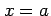 において極大値
において極大値 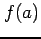 をとるという.
をとるという.
-
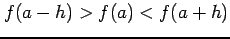 をみたすとき,
関数
をみたすとき,
関数  は点
は点 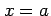 において極小値
において極小値 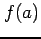 をとるという.
をとるという.
定理 5.58 (微分係数と増減,極値)
微分係数と関数の増減および極値の関係に関して次のことがいえる.
を得る.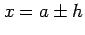 とおくと
とおくと
となる.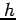 を十分小さな正の値として考える.
を十分小さな正の値として考える.
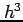 以降の項は十分小さく無視できる.
以降の項は十分小さく無視できる.
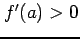 のとき
のとき
が成り立つので,テイラー展開の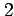 次の項を無視しすれば
次の項を無視しすれば
を得る.よって は増加の状態にある.
次に
は増加の状態にある.
次に 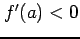 のとき,同様に
のとき,同様に
となるので, は減少の状態にある.
次に
は減少の状態にある.
次に 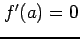 ,
, 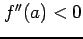 のとき,
のとき,
となるので, は
は 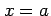 において極大値をとる.
最後に
において極大値をとる.
最後に 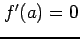 ,
, 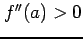 のとき,
のとき,
となるので, は
は 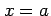 において極小値をとる.
において極小値をとる.
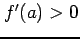 のとき,
のとき,
 は点
は点 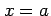 において
増加の状態にある.
において
増加の状態にある.
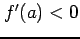 のとき,
のとき,
 は点
は点 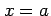 において
減少の状態にある.
において
減少の状態にある.
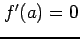 ,
, 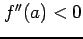 のとき,
のとき,
 は点
は点 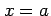 において極大値をとる.
において極大値をとる.
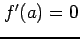 ,
, 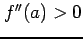 のとき,
のとき,
 は点
は点 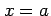 において極小値をとる.
において極小値をとる.
(証明)
関数 ![]() をテイラー展開して
をテイラー展開して
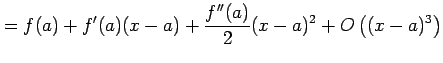 |
を得る.
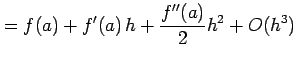 |
||
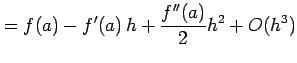 |
となる.
が成り立つので,テイラー展開の
を得る.よって
となるので,
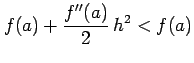 |
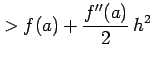 |
|
となるので,
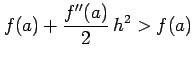 |
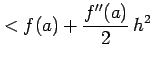 |
|
となるので,
定理 5.59 (単調増加)
関数  が定義域内の任意の点で
が定義域内の任意の点で 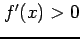 であるとき,
であるとき,
 は単調増加である.
は単調増加である.
定理 5.60 (単調減少)
関数  が定義域内の任意の点で
が定義域内の任意の点で 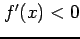 であるとき,
であるとき,
 は単調減少である.
は単調減少である.
平成19年10月3日