4.16 直交変換
定義 4.74 (直交変換)
内積空間 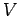 において,
線形変換
において,
線形変換 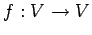 ;
;
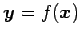 が
が
をみたすとき, を直交変換(orthogonal transformation)という.
を直交変換(orthogonal transformation)という.
をみたすとき,
定理 4.75 (直交変換)
内積空間 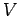 において,
において,
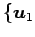 ,
,  ,
,
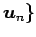 を
正規直交基底とする.
線形変換
を
正規直交基底とする.
線形変換 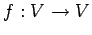 ;
;
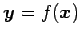 が
直交変換となるための必用十分条件は,
が
直交変換となるための必用十分条件は,
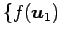 ,
,  ,
,
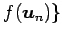 が
正規直交基底となることである.
が
正規直交基底となることである.
(十分条件)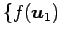 ,
,  ,
,
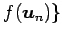 を
正規直交基底とする.
なすわち,
を
正規直交基底とする.
なすわち,
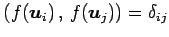 とする.
任意のベクトル
とする.
任意のベクトル
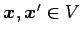 は
は
と表される. このとき
となる. よって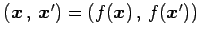 を得る.
を得る.
(証明)
(必用条件)
![]() が直交変換であれば
が直交変換であれば
![]() となるで,
となるで,
(十分条件)
と表される. このとき
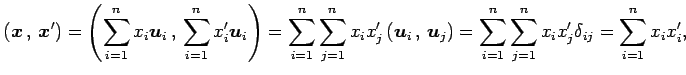 |
||
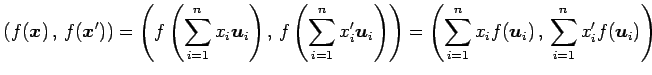 |
||
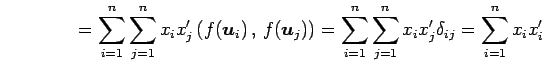 |
となる. よって
定理 4.76 (直交変換の内積の不変性)
線形変換  が直交変換であるための必用十分条件は
が直交変換であるための必用十分条件は
である.
と表す. このとき
となる.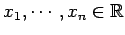 は任意であり,
恒等式
は任意であり,
恒等式
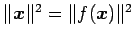 が成り立つためには
が成り立つためには
をみたす必要がある. よって, ,
,  ,
,
 は
正規直交基底であり,
は
正規直交基底であり, は直交変換となる.
は直交変換となる.
である.
(証明)
(必用条件)
![]() が直交変換であれば
が直交変換であれば
![]() であるから,
であるから,
![]() とおくと,
とおくと,
![]() となり,
となり,
![]() を得る.
(十分条件)
を得る.
(十分条件)
![]() ,
, ![]() ,
,
![]() を正規直交基底とする.
任意のベクトル
を正規直交基底とする.
任意のベクトル ![]() を
を
と表す. このとき
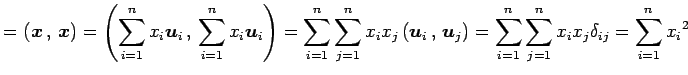 |
||
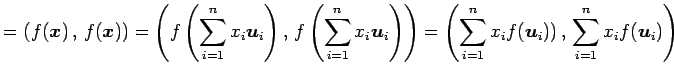 |
||
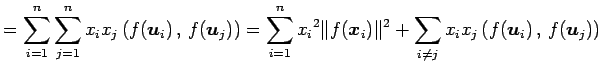 |
となる.
をみたす必要がある. よって,
注意 4.77 (直交変換のノルムの不変性)
直交変換  において,長さは不変である.
において,長さは不変である.
定理 4.78 (直交変換の角の不変性)
直交変換  において,角度は不変である.
において,角度は不変である.
を得る.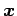 ,
, 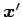 のなす角と
のなす角と
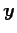 ,
,  のなす角とは等しい.
のなす角とは等しい.
(証明)
![]() ,
,
![]() とおく.
とおく.
![]() ,
,
![]() ,
,
![]() より,
より,
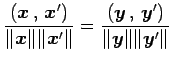 |
を得る.
注意 4.79 (合同変換)
直交変換は合同変換のひとつである.
合同変換(congruent transformation)とは,
長さと角を不変に保つ変換のことをいう.
合同変換で写される図形は,変換前の図形と後の図形とは合同となる.
また,角を不変に保ち,長さはある定数倍になる変換のことを
相似変換(similarity transformation)という.
角を不変に保つ変換を等角変換(isometric transformation)という.
注意 4.80 (合同変換)
回転変換と鏡映変換は合同変換である.
Kondo Koichi

平成18年1月17日