4.15 直交行列と正規直交系
定理 4.69 (直交行列と正規直交系)
行列  が直交行列であることと,
行列
が直交行列であることと,
行列  の列ベクトルまたは行ベクトルが正規直交系であることとは,
必要十分条件である.
の列ベクトルまたは行ベクトルが正規直交系であることとは,
必要十分条件である.
とおく.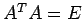 より,
より,
となるので,
を得る. 行ベトクルに対しても同様の操作で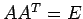 より示される.
より示される.
(証明)
直交行列 ![]() を列ベクトルに分割し
を列ベクトルに分割し
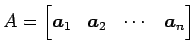 |
とおく.
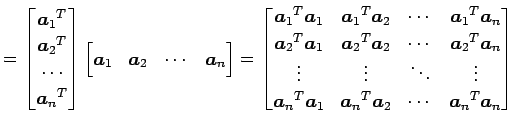 |
||
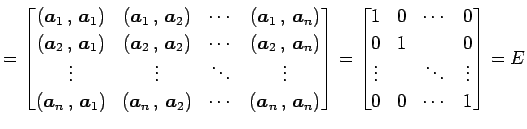 |
となるので,
を得る. 行ベトクルに対しても同様の操作で
定理 4.70 (直交行列と正規直交基底)
内積空間 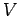 において,
において,
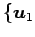 ,
,  ,
,
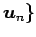 と
と
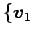 ,
,  ,
,
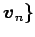 を正規直交基底とする.
このとき,基底
を正規直交基底とする.
このとき,基底
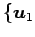 ,
,  ,
,
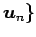 から
から
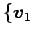 ,
,  ,
,
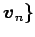 への
変換行列
への
変換行列 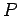 は直交行列となる.
は直交行列となる.
と書ける.これより,
である. この式と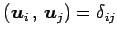 より
より
を得る.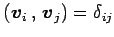 より
より
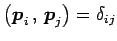 が成り立つ.
が成り立つ.
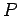 の列ベクトルが正規直交系となるので,
の列ベクトルが正規直交系となるので,
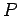 は直交行列である.
は直交行列である.
(証明)
![]() は基底の変換行列なので,
は基底の変換行列なので,
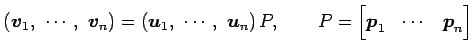 |
と書ける.これより,
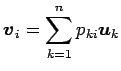 |
である. この式と
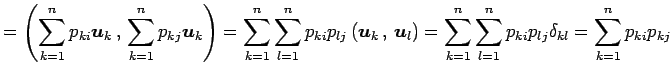 |
||
を得る.
問 4.71 (直交行列の具体例)
次の行列は直交行列であることを示せ.
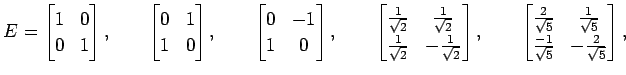 |
||
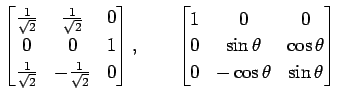 |
問 4.72 (直交行列の具体例)
直交行列
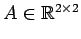 はすべて
はすべて
の形で表される. これを示せ.
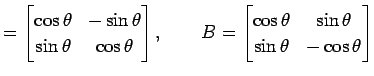 |
の形で表される. これを示せ.
例 4.73 (直交行列の具体例)
グラム・シュミットの直交化法で正規直交化されたベクトル
を列ベクトルとして並べた行列
は直交行列となる.
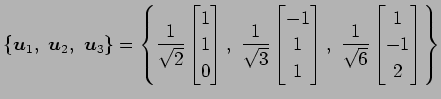 |
を列ベクトルとして並べた行列
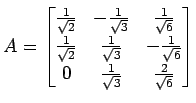 |
は直交行列となる.
Kondo Koichi

平成18年1月17日