3.39 正規直交基底における座標
定理 3.152 (正規直交基底における 1 次結合)
内積空間 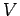 において,
基底
において,
基底
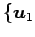 ,
,
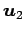 ,
, 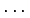 ,
,
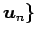 が
正規直交基底であれば,
任意のベクトル
が
正規直交基底であれば,
任意のベクトル 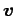 は
は
と表される.
の両辺との内積をとると
を得る.
と表される.
(証明)
ベクトル ![]() と
と
の両辺との内積をとると
を得る.
例 3.153 (正規直交基底における 1 次結合)
 の点
の点 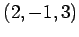 は,
標準基底
は,
標準基底
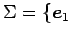 ,
, 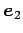 ,
,
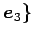 における座標であり,正確に書くと
における座標であり,正確に書くと
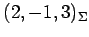 である.
この点の位置ベクトルは
である.
この点の位置ベクトルは
となる. 正規直交基底
における座標を求める. なすわち,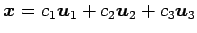 の係数
の係数
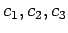 を求める.
を求める.
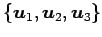 は
正規直交基底であるから,
は
正規直交基底であるから,
より
を得る. よって
と表される. 基底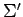 における座標は
における座標は
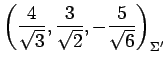 である.
である.
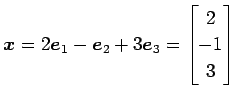 |
となる. 正規直交基底
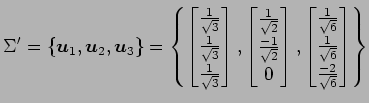 |
における座標を求める. なすわち,
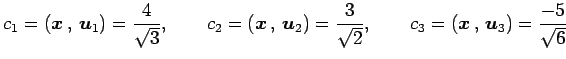 |
より
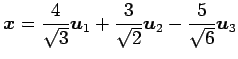 |
を得る. よって
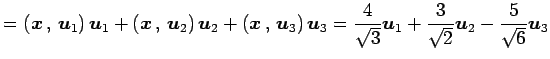 |
と表される. 基底
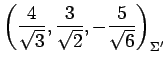 である.
である.
定理 3.154 (正規直交基底における内積)
内積空間 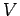 において,
において,
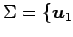 ,
, 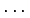 ,
,
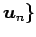 を
正規直交基底とする.
ベクトル
を
正規直交基底とする.
ベクトル 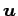 ,
,
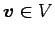 の
座標をそれぞれ
の
座標をそれぞれ
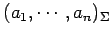 ,
,
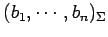 とする.
このとき
とする.
このとき
が成り立つ.
と表される.このとき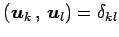 より
より
を得る.
が成り立つ.
(証明)
![]() ,
,
![]() は
は
と表される.このとき
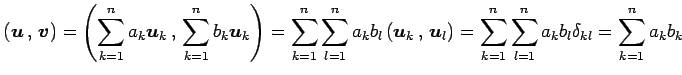 |
を得る.
Kondo Koichi

平成18年1月17日