3.22 一般の場合での 1 次独立なベクトルの最大個数
定理 3.82 ( 1 次独立なベクトルと行列)
ベクトル 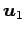 ,
, 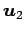 ,
,  ,
,
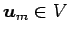 が
1 次独立であり,
ベクトル
が
1 次独立であり,
ベクトル 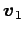 ,
, 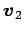 ,
,  ,
,
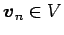 が
が
をみたす.
となる.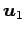 ,
,  ,
, 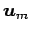 は 1 次独立であるから,
は 1 次独立であるから,
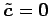 となる.
となる.
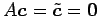 より
より
を得る. これは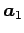 ,
, 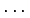 ,
, 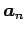 の 1 次関係である.
(ii)
の 1 次関係である.
(ii) 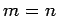 のとき
のとき 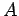 は正方行列であるから,
は正方行列であるから,
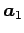 ,
,  ,
, 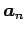 が 1 次独立であることと
が 1 次独立であることと
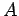 が正則であることは等価である.
が正則であることは等価である.
をみたす.
- (i).
-
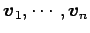 の 1 次関係と
の 1 次関係と
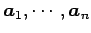 の 1 次関係は等しい.
の 1 次関係は等しい.
- (ii).
- 特に
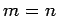 のとき,
のとき,
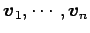 が 1 次独立であることと,
が 1 次独立であることと,
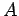 が正則であることとは,必用十分条件である.
が正則であることとは,必用十分条件である.
(証明)
(i)
ベクトル ![]() ,
, ![]() ,
, ![]() の
1 次関係は
の
1 次関係は
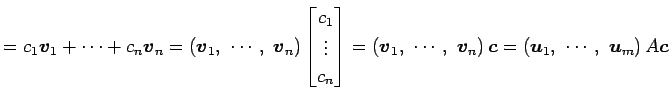 |
||
となる.
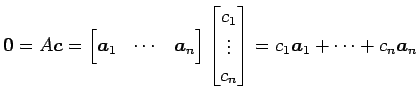 |
を得る. これは
例 3.83 ( 1 次独立なベクトルと行列)
ベクトル空間
![$ \mathbb{R}[x]_3$](img554.png) のベクトル
のベクトル
が 1 次独立であるか調べる. まず,ベクトル![$ 1,x,x^2,x^3\in\mathbb{R}[x]_3$](img1062.png) は明らかに 1 次独立である.
このとき
は明らかに 1 次独立である.
このとき
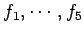 と
と
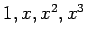 とは
とは
の関係にある. 次に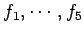 の 1 次関係は
の 1 次関係は
と表される. (☆)を用いると
となり,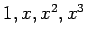 に関する 1 次関係を得る.
に関する 1 次関係を得る.
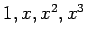 は 1 次独立であるから
は 1 次独立であるから
 が
成立する.
よって
が
成立する.
よって  は
は
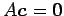 をみたす.
をみたす.
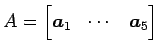 とおくと,
とおくと,
となるので,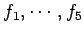 と
と
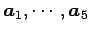 の
1 次関係は等しい.
ここで,行列
の
1 次関係は等しい.
ここで,行列 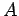 を簡約化して
を簡約化して
とおく. このときある正則行列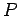 を用いて
を用いて 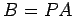 と表されるから,
と表されるから,
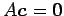 より
より
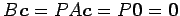 が成り立つので,
が成り立つので,
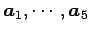 と
と
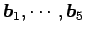 の 1 次関係は等しい.
よって,
の 1 次関係は等しい.
よって,
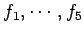 の 1 次関係は
の 1 次関係は
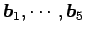 の 1 次関係より定まる.
の 1 次関係より定まる.
より,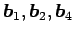 は 1 次独立である.
は 1 次独立である.
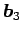 ,
, 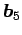 は
は
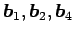 の
1 次結合で表される.
よって
の
1 次結合で表される.
よって
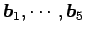 の 1 次独立なベクトルの
最大個数は
の 1 次独立なベクトルの
最大個数は
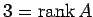 である.
行列
である.
行列 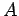 の列ベクトルに対しても同じ 1 次関係が成り立つので,
の列ベクトルに対しても同じ 1 次関係が成り立つので,
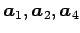 は 1 次独立である.
残りのベクトルは
は 1 次独立である.
残りのベクトルは
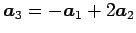 ,
,
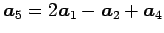 と 1 次結合で表される.
と 1 次結合で表される.
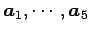 の 1 次独立なベクトルの
最大個数は
の 1 次独立なベクトルの
最大個数は
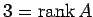 である.
である.
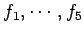 にも同じ 1 次関係が成り立つので,
にも同じ 1 次関係が成り立つので,
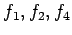 は 1 次独立である.
残りのベクトルは
は 1 次独立である.
残りのベクトルは
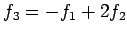 ,
,
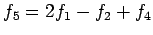 と 1 次結合で表される.
よって
と 1 次結合で表される.
よって
 の
1 次独立なベクトルの最大個数は
の
1 次独立なベクトルの最大個数は
 である.
である.
が 1 次独立であるか調べる. まず,ベクトル
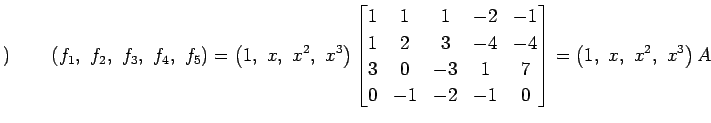 |
の関係にある. 次に
| 0 | 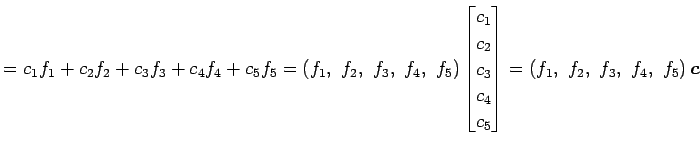 |
と表される. (☆)を用いると
となり,
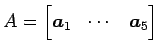 とおくと,
とおくと,
となるので,
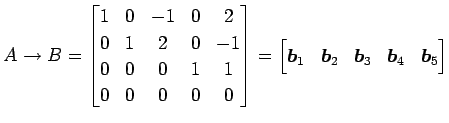 |
とおく. このときある正則行列
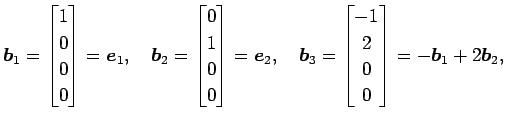 |
||
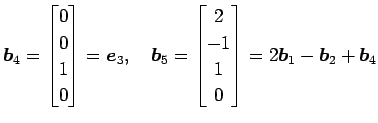 |
より,
Kondo Koichi

平成18年1月17日