3.21 1 次独立なベクトルの最大個数と行列の正則性
定理 3.81 (行列と 1 次独立性)
正方行列
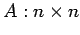 に対して次の関係が成り立つ:
に対して次の関係が成り立つ:
| |
||
| |
||
| |
||
Kondo Koichi

平成18年1月17日
3.21 1 次独立なベクトルの最大個数と行列の正則性
定理 3.81 (行列と 1 次独立性) 正方行列に対して次の関係が成り立つ:
の
個の列ベクトルは 1 次独立
の
個の行ベクトルは 1 次独立
: 正則行列(
は逆行列をもつ)
Kondo Koichi


平成18年1月17日