5.31 直交行列の対角化
定理 5.105 (直交行列の固有値)
直交行列の固有値は絶対値が 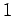 となる複素数である.
となる複素数である.
が成り立つ. ここで,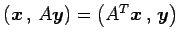 を用いた.
を用いた.
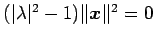 ,
,
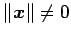 より,
より,
 が成立する.
が成立する.
(証明)
![]() ,
,
![]() とし,
とし,
![]() 上の内積を用いて,
上の内積を用いて,
が成り立つ. ここで,
注意 5.106 (直交行列)
直交行列は正規行列である.
定理 5.107 (直交行列の固有ベクトル)
直交行列において,
異なる固有値に属する固有ベクトルは直交する.
となる. ここで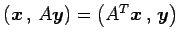 を用いた.
を用いた.
であるから,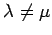 より
より
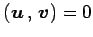 を得る.
を得る.
(証明)
直交行列は正規行列であるので固有ベクトルは直交する.
または,次のように示す.
![]() であり,
固有値は複素平面の単位円上にあるから,
であり,
固有値は複素平面の単位円上にあるから,
![]() ,
,
![]() ,
,
![]() (
(
![]() ) とする.
) とする.
![]() 上の内積を用いて,
上の内積を用いて,
となる. ここで
であるから,
定理 5.108 (直交行列の対角化)
直交行列
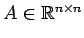 の
固有値を
の
固有値を
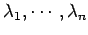 とする.
このとき,
とする.
このとき,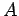 は
ユニタリー行列
は
ユニタリー行列
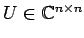 を用いて
を用いて
と対角化される. ただし,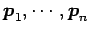 は
は
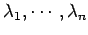 の固有ベクトルであり,
の固有ベクトルであり,
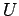 がユニタリー行列となるように選ぶとする.
がユニタリー行列となるように選ぶとする.
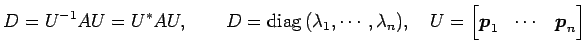 |
と対角化される. ただし,
定理 5.109 (直交行列の実標準形)
直交行列
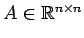 の
固有値を
の
固有値を
とする. このとき,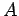 は
直交行列
は
直交行列
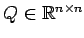 を用いて
を用いて
と実標準形でブロック対角化される. ただし,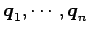 は
は
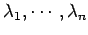 の固有ベクトルであり,
の固有ベクトルであり,
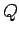 が直交行列となるように選ぶとする.
が直交行列となるように選ぶとする.
とする. このとき,
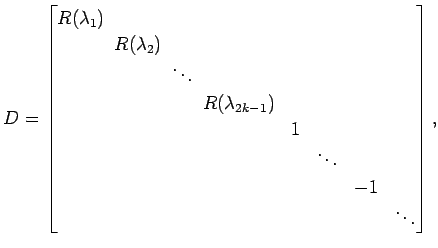 |
||
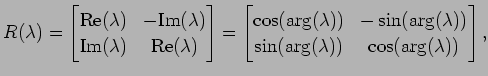 |
||
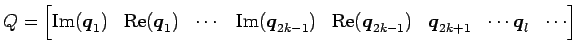 |
と実標準形でブロック対角化される. ただし,
例 5.110 (直交行列の対角化の具体例)
行列
を対角化する.
より,固有値は
である.
より,固有ベクトルはそれぞれ
となる.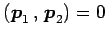 であるから,
規格化して
であるから,
規格化して
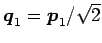 ,
,
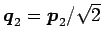 とする.
このとき
とする.
このとき 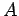 はユニタリー行列
はユニタリー行列 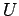 を用いて
を用いて
と対角化される. 実標準系では
となる.
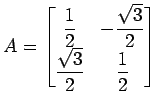 |
を対角化する.
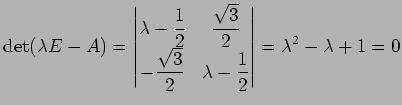 |
より,固有値は
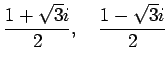 |
である.
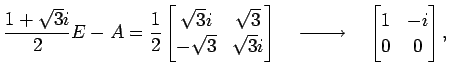 |
||
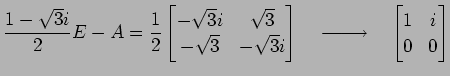 |
より,固有ベクトルはそれぞれ
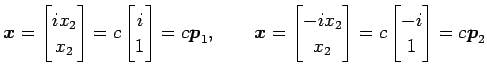 |
となる.
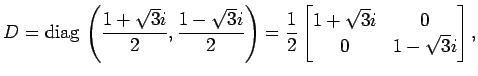 |
||
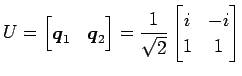 |
と対角化される. 実標準系では
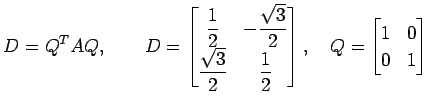 |
となる.
Kondo Koichi

平成18年1月17日